يقول الفلكي والفيزيائي وعالم الرياضيات “غاليليو غاليلي” في خطابه الذي ألقاه في دار ألابرا في إيطاليا:

“لا يمكننا فهم الكون حتى نتعلم اللغة المكتوب بها، ونصبح على دراية بكل معاني تلك اللغة؛ فلغة الكون هي الرياضيات، حيث تمثل الرموز والمثلثات والدوائر والأشكال الهندسية الأخرى معانٍ مختلفة للكون، وبدون تلك اللغة، فهذا يعني أنه من المستحيل إنسانيًا فهم كلمة واحدة.”

وختم غاليليو خطابه باقتباسه المشهور:

“الرياضيات هي اللغة التي كتب بها الله الكون.”

وعليه، هل حقا تعتبر الرياضيات لغة نتحدث بها، مثل الإنجليزية أو العربية أو الصينية؟ للإجابة على هذا السؤال يجب علينا أولًا أن نضع تعريفًا للغة، ومعرفة كيف يتم استخدام المفردات والمعاني والقواعد لبناء الجمل في أي لغة.

ما هي اللغة؟

هناك تعريفات متعددة لـ”اللغة”. قد تكون اللغة عبارة عن نظام من الكلمات أو الرموز المستخدمة للتعبير عن شيء ما داخل نظام ما، وقد تشير اللغة إلى نظام اتصال باستخدام الرموز أو الأصوات، يعرّف اللغوي نعوم تشومسكي اللغة بأنها مجموعة من الجمل المبنية باستخدام مجموعة محدودة من العناصر، ويعتقد بعض اللغويين أن اللغة يجب أن تكون قادرةً على تمثيل الأحداث والمفاهيم المجردة.

أيًّا كان التعريف المستخدم والمتداول، يجب على أي لغة أن تحتوي على المكونات التالية:

• مفردات اللغة، يجب أن يكون هناك مفردات من الكلمات أو الرموز في أي لغة.
• معاني، يجب أن يكون للكلمات أو الرموز معنًى حتى يتم استخدامها في اللغة.
• قواعد، يجب أن تحتوي أي لغة على قواعد، وهي مجموعة من “القوانين” التي توضح كيفية استخدام المفردات.
• الصياغة النحوية، تنظم الصياغة النحوية الرموز أو الكلمات لتكوين الهيكل الخاص بكل لغة.
• يتكون السرد أو الحوار من سلاسل من الافتراضات النحوية.
• يجب أن يكون هناك مجموعةٌ من الأشخاص الذين يستخدمون تلك الكلمات أو الرموز ويفهمونها.

ولحسن الحظ، أن الرياضيات تفي بكل تلك المتطلبات من رموز وقواعد ومعانٍ وصياغة لتلك الرموز، وأيضًا يتم استخدامها من قبل مجموعة من الأشخاص يطلق عليهم “علماء الرياضيات”.

على الرغم من أن الرياضيات تستخدم في توصيل مفاهيم الطبيعة، إلا إنها تصف نفسها تلقائيًا فيما يعرف باسم “ما وراء الرياضيات- metamathematics”.

المفردات والقواعد والصياغة اللغوية في الرياضيات

تعتمد مفردات الرياضيات على العديد من الأبجديات المختلفة، بالإضافة إلى بعض الرموز الخاصة بالرياضيات.

يمكن لأي شخص قراءة أي معادلة رياضية عن طريق تشكيلها على شكل جملة تحتوي على اسم وفعل، تماما مثل الجملة في اللغات المحكية، فمثلا:

3 + 5 = 8

يمكن اعتبارها “ثلاثة أضيف إليها خمسة، فأصبحت تساوي ثمانية”.

• وعلى هذا المنوال، فإن الرياضيات تتضمن بعض الأسماء:

الأرقام العربية (1، 2، 3، 7، 5، 0)

الكسور (1⁄4، 5⁄9، 1⁄3)

المتغيرات (a، b ، c، x ، y ، z)

التعبيرات (3x، 4+ x)

الرسوم البيانية أو الهندسية (دائرة، زاوية، مثلث، تنسور، مصفوفة)

المالانهاية (∞)

الأعداد التخيلية (i، -i)

سرعة الضوء (c)

• بالإضافة إلى الأسماء، فالرياضيات تتضمن أيضًا مجموعة من الأفعال كالآتي:

التساوي أو التباين (=، <، >)

إجراءات، مثل الجمع والطرح والضرب والقسمة (+، -، x أو *، ÷ أو /)

عمليات أخرى (sin، cos، tan، sec)

إذا حاولت إنشاء مخطط جملي على أي عبارة رياضية، فبالتأكيد ستحصل على مصادر، وعطف، وصفات، إلخ، كما هو الحال في اللغات الأخرى؛ حيث يعتمد الدور الذي يلعبه الرمز على السياق الخاص بالجملة أو العبارة الرياضية.

وأيضا القواعد والصياغة اللغوية في الرياضيات لا تختلف كثيرًا عن المفردات؛ فهي قواعد دولية، بغض النظر عن البلد الذي تنتمي إليه أو اللغة التي تتحدثها، فإن بنية اللغة الرياضية هي نفسها لا تتغير.

• حيث يتم قراءة الصيغ من اليسار إلى اليمين، ويتم استخدام الأبجدية اللاتينية وأحيانًا اليونانية للمعاملات والمتغيرات فقط، وعادةً ما يتم تمثيل الأعداد صحيحة بواسطة i، j، k، l، m، n، ويتم تمثيل الأرقام الحقيقية بواسطة a،b ،c ،α ،β، γ، ويتم الإشارة إلى الأرقام المركبة بواسطة w و z، المجاهيل بواسطة x، y، z، وأسماء الدوال عادة ما تكون f ،g ،h.
• تستخدم الأبجدية اليونانية أيضًا لتمثيل مفاهيم معينة. على سبيل المثال، يستخدم λ للإشارة إلى طول الموجة، وρ للإشارة إلى الكثافة.
• تشير الأقواس إلى ترتيب تتفاعل فيه الرموز والارقام.

 الحجة ضد الرياضيات كلغة

لا يتفق الجميع على أن الرياضيات لغة. بعض تعريفات “اللغة” تصفها بأنها شكل اتصال منطوق، في حين أن الرياضيات هي شكل مكتوب من التواصل، على الرغم من أنه قد يكون من السهل قراءة عبارة جمع بسيطة بصوت عالٍ (على سبيل المثال، 1 + 1 = 2)، فإنه من الأصعب قراءة معادلات أخرى بصوت عالٍ (على سبيل المثال، معادلات ماكسويل).

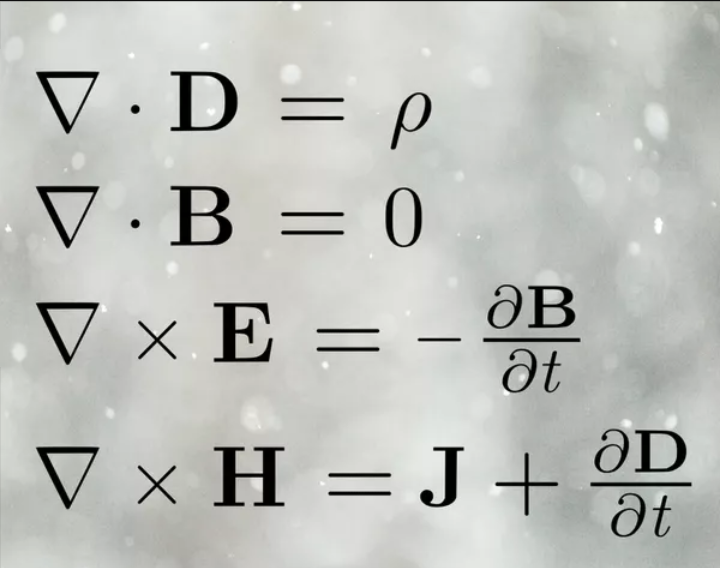
أيضًا، سيتم تقديم البيانات المنطوقة في اللغة الأم للمتكلم، وليس بلغة عالمية.

ولكن إذا أخذنا بهذا التعريف، سيتم أيضًا استبعاد لغة الإشارة استنادًا إلى هذا المعيار، ولكن معظم اللغويين يقبلون لغة الإشارة كلغة حقيقية.

اللغة كأداة تعليمية

فهم كيفية عمل الجمل الرياضية مفيد ومهم عند تدريس أو تعلم الرياضيات، غالبًا ما يعثر الطلاب على أرقام ورموز مُخيفة، لذا فإن وضع معادلة في لغة مألوفة يجعل الموضوع أكثر سهولة، فالأمر يشبه ترجمة لغة أجنبية إلى لغة معروفة.

وبما أن الطلاب لا يحبون عادة المسائل ذات الطابع اللغوي، فإن استخراج الأسماء والأفعال والصفات من اللغة المنطوقة / المكتوبة وترجمتها إلى معادلة رياضية هي مهارة ثمينة ومفيدة؛ حيث تساعد على الفهم، وتزيد من مهارات حل المشكلات لدى الطلاب.

ولأن الرياضيات هي نفسها في جميع أنحاء العالم، فإن الرياضيات تصبح بمثابة لغة عالمية؛ العبارة أو الصيغة لها نفس المعنى، بغض النظر عن اللغة الأخرى التي تصاحبها. وبهذه الطريقة، يمكن أن تساعد الرياضيات الناس على التعلم والتواصل، حتى لو كانت هناك حواجز اتصال أخرى.