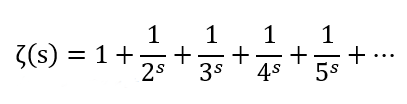مسائل الألفية: فرضية ريمان والمليون دولار!

“تم إثبات فرضية ريمان” الخبر الذي قلب مجتمع علماء الرياضيات رأسًا على عقب

• ماذا تعرف عن فرضية ريمان؟

   فرضية ريمان هي أحد مشاكل الألفية التي حددها معهد كلاي الرياضي عام 2000، والتي يكفي حل واحدة منها فقط لتربح مليون دولار نقدًا في الحال.

لكن الغريب في الأمر أنه لم يحل من تلك المشاكل سوى مشكلة واحدة حتى الآن، وهي إثبات صحة حدسيه بوانكاريه. من المثير للدهشة أن صاحب الحل -غريغورى بيرلمان- رفض أخذ المليون دولار معلّلًا ذلك بأن اهتمامه لا يكون سوى للرياضيات.

حلت فرضية ريمان محل نظرية فيرمات الأخيرة في كونها المشكلة الأكثر شهرة في الرياضيات، وذلك بعد حل نظرية فيرمات من قبل إثنين من علماء الرياضيات في التسعينات.

ولفهم  فرضية ريمان علينا أولًا التعرّف على دالة زيتا لريمان، وهي ببساطة دالة تعيّن قيمة معينة لكل رقم وهذه القيمة تحدد من العلاقة الآتية:

 

اقترح ريمان أنه يمكن التعويض عن S ليس فقط بالأرقام الصحيحة أو حتى الحقيقية وإنما أيضًا بالأرقام المركبة.

والأعداد المركبة هي أعداد ببساطة تتكون من شقّين شق حقيقي وشقّ تخيّلي. التخيّلي عبارة عن -1√.

والذي نسميه i، أو ت فيما إذا كنت تدرسها بالعربية.

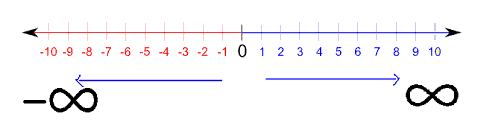
عندما نتخيل خط الأعداد الحقيقية فإننا نرسم في مخيّلتنا خطأ موزّع عليه الأرقام من سالب ما لا نهاية إلى ما لانهاية، كالآتي:

لكن ماذا لو أردنا إضافة الأعداد المركبة أيضًا؟

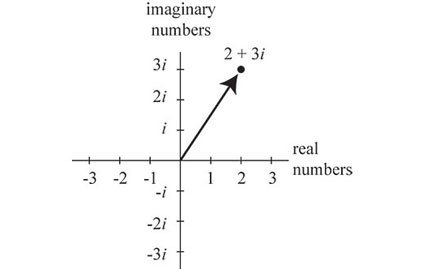
يصبح الأمر كالتالي:

نلاحظ أن النقطة المشار إليها عبارة عن عدد ويساوى 2+3i

في البداية ظن ريمان أن S يمكن التعويض عنها بأي رقم 2 أو 3 أو 4 إلى آخره، ومن ثم يقترب الناتج من قيمة معينة يمكن تحديدها.

وهذا يعني ببساطة أن الدالة معرّفة لكل من تلك القيم.

ثم أدرك فيما بعد أن أي قيمة ل S ستنتج قيمة معرفة لدالة زيتا طالما أن قيمة S تقع على الجانب الأيمن من الخط الرأسي الذي يمر بالواحد، وهذا يعني أنّ أيّ قيمة أكبر من الواحد تكون عندها الدالة معرّفة، أمّا غير ذلك تكون الدالة غير معرفة.

وبطريقة ما، وجد ريمان وسيلة لتوسيع مدى الأعداد التي تجعل الدالة معرّفة ليشمل المستوى كله. لكنها مع ذلك بقيت غير معرفة عند نقطة واحدة فقط يسميها علماء الرياضيات الفجوة أو المفردة، عندها لا تكون الدالة معرّفة أيّ أنها لا تتقرب إلى أيّ قيمة يمكننا تحديدها، هذه النقطة هي الواحد، أيّ أن الدالة معرّفة على المستوي كله ما عدا النقطة 1

أما الطريف في الأمر هو أننا نفكر دائمًا أن الواحد هو أسهل الأرقام سواء من ناحية الضرب أو الجمع أو القسمة لكنه يأتي هنا ليصبح مشكلة الدالة الوحيدة، فالدالة ستكون معرّفة مثًلا عند i ولا تكون معرفة عند الواحد.

 • لكن ما هو سؤال المليون دولار؟

السؤال ببساطة هو ماهي “أصفار الدالة ” أو القيم التي يمكن التعويض بها داخل الدالة وتجعل قيمة الدالة صفر؟

هناك بعض الأصفار الواضحة للدالة على سبيل المثال -2,-4,-6. وبعبارة أخرى الأرقام الزوجيّة السالبة تجعل الدالة صفر. لكن هذا لم يكن السؤال بالضبط السؤال هو ما الأصفار الأخرى للدالة؟

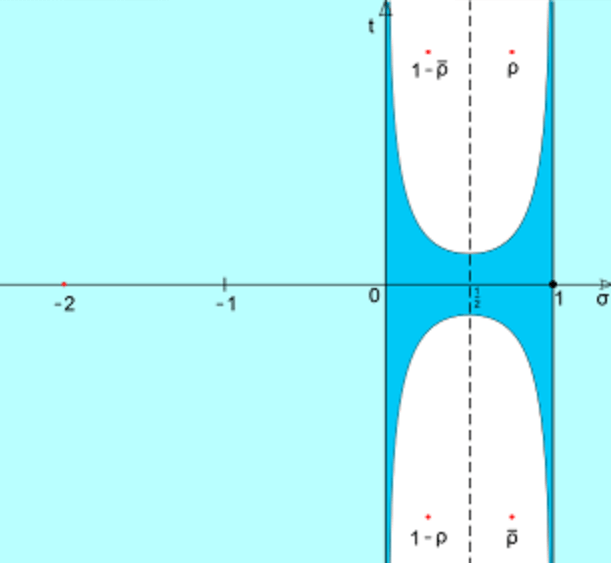
افترض ريمان منطقة تقع فيها كل الأصفار الغير واضحة للدالة وهي المنطقة ما بين الخط الرأسي الذي يمر بالصفر والخط الرأسي الذي يمرّ بالواحد ثم وضع فرضًا ظريفًا.

يقول الفرض أن كل الأصفار الغير واضحة للدالة تقع على الخط الرأسي الذي يمر بالنقطة 0.5 ويسمى بالخط الحرج.

 

في الحقيقة بطريقة ما كنا نعلم أن كل أصفار الدالة ستكون في تلك المنطقة بين الخط الرأسي الذي يمر بالواحد والخط الرأسي الذي يمر بالصفر.

لكن السؤال هو هل حقًا ستكون جميع الأصفار على هذا الخط؟

مؤخرًا وبعد 9 سنوات من العمل أعلن اثاناسيوس فوكاس عالم الرياضيات من قسم الرياضيات التطبيقية والفيزياء النظرية بجامعة كامبريدج عن طريقة جديدة تقترح حلًا لهذه المشكلة وذلك عن طريق فرضية ليندلوف.

• لكن ما علاقة فرضية ليندلوف بفرضية ريمان؟!

فرضية ليندلوف تعمل على تخمين معدل نمو دالة ريمان زيتا على الخط الحرج وتعتبر واحدة من أشهر المشاكل التي لم تحل والمتصلة بالأعداد الأولية.

توضح فرضية ليندلوف جزءا كبيرا من فرضية ريمان وبالتالي فإن فرضية ريمان تعني ضمنيًّا فرضية ليندلوف

يقول فوكاس:

” أن دالة زيتا تعتمد فقط على المتغير s، وحاليًا يمكن التحقق من صحة فرضية ريمان بواسطة كمبيوتر Core I 10 حتى الأس الثالث عشر للمتغير s، وهو رقم كبير جدًّا لكنه لايزال صغيرا مقارنة بال “مالا نهاية” وهذا إن دلّ على شيء يدل على حاجتنا لفهم تصرف الدالة زيتا عند أرقام عالية جدًّا وهذا تمامًا ما تفعله فرضية ليندلوف”

يكمل فوكاس قائلًا: “إن النهج الذي اتخذته الدالة كان نهجا مختلفا تماما عن النهج العادي، في البداية قمت بتضمين دالة زيتا ضمن مشكلة أكبر ثم وجدت أن دالة زيتا تحل مشكلة مهمة جدًّا في التحليل المعقد أو ما يعرف باسم Complex analysis تسمى مشكلة “ريمان –هيلبرت“، ثم قمت بعمل الحسابات اللازمة لتحديد تصرف المتغير s عند قيم كبيرة على الرغم من كون هذا النهج سهل في التحدث عنه إلى أن العمل عليه بطريقة تقنية صعب جدًّا بسبب تحليل مشكلة ريمان-هلبرت”.

بهذه الطريقة استطاع فوكاس إثبات صحة فرضية ريمان. لكن ما أهمية إثبات صحة الفرضية من عدمها على أيّ حال؟

تعتبر دالة ريمان زيتا أداة سحرية في فرع نظرية الأعداد والتي تستخدم للتحقيق من خصائص الأعداد الأولية، وفهم توزيع الأعداد الأوليّة نفسها مهم جدًّا في مسألة التشفير حيث أن الأعداد الأوليّة هي حرفيًا “المفاتيح” السرية التي تخفي أحدث ما لديك من عمليات شراء عن أعين المتطفلين.

وقد ساعدت دالة ريمان زيتا على الفهم العلمي للعديد من المجالات الأخرى، كالبيولوجيا والكيمياء والفيزياء، وكل ذلك دون وجود إثبات أو دليل رسمي على فرضية ريمان الشهيرة.

وقد كتب عالم الرياضيات النظرية إنريكو بومبيري:

“إن فشل فرضية ريمان سيخلق فوضى في توزيع الأعداد الأولية.”

إذ كانت فرضية ريمان -منذ نشرها- هي المحور الرئيسي لنظرية الأعداد الأولية والسبب الرئيسي لإثبات وجود شيء يسمى نظرية العدد الأولي في عام 1896. فهذا يعني أن فوكاس قد قدّم خدمة عظيمة للعلوم بإثباته لصحة الفرضية، هذا الرجل الذي هو في الأساس خبير عالمي في المقاربات، وهو فرع تطبيقي في الرياضيات يساعد الرياضيين على الإجابة عن سؤال “كيف تتصرف الدالة عندما يكون المتغير الخاص بها كبير جدًّا”

وربما يساعد فوكاس على تحقق تقدما كبيرًا في فهمنا لتعقيد الخوارزميات أو ما يعرف باسم التشفير-وهو فرع مهم في علوم الحاسب- نتيجة عمله على فرضية ليندلوف.

فمعرفة تعقيد خوارزمية ما يسمح لنا بإجابة سؤال مثل كم المدة الزمنية التي سيستغرقها الحاسب لتشغيل خوارزمية بعدد مدخلات معيّن والمساحة التي سيشغلها من الذاكرة وهل المشكلة قابلة للحل أم لا؟

في الواقع لم يكن هذا إنجاز فوكاس الوحيد فطريقته المعروفة بـ “طريقة فوكاس” لحل معادلات التفاضلات الجزئية أو ما يعرف باسم partial differential equation حلّت بالكامل محل طرق التحويل أو ما يعرف باسم Transformation methods  التي اُكتشفت واُستخدمت من القرن ال18 لقرابة 250 عامًا.

 

في النهاية لا يسعنا القول سوى هنيئًا للبشرية بهذا الإنجاز..