اللانهاية ومفارقاتها

“لا يستطيع أن يطردنا أحد من الجنّة التي خلقها لنا جورج كانتور” ديفيد هيلبرت
يسأل زينون الإيلائي إذا كان بمقدور أخيل، العداء السريع، أن يلحق بسلحفاة تسبقه. ليلحق أخيل بالسلحفاة عليه أن يصل أولاً إلى مكانها في هذه اللحظة ولتكن ت1، ولكن السلحفاة ستكون قطعت شوطاً إلى مكان آخرفعليه أن يصله في ت2، ولكن السلحفاة ستكون قطعت مسافة أخرى، حتى لو كانت أصغر، فعليه أن يلحقها في ت3. وهكذا تباعاً، فكلما يصل لنقطة سبق للسلحفاة وكانت فيها، سيجد أنها تجاوزتها ولو بمسافة تقل بشكل مستمر، لكنها تبقى موجودة طالما أننا يمكن أن نعد بشكل لا نهائي هذه النقط التي يصل إليها أخيل في اقترابه من السلحفاة. فأخيل يقترب من السلحفاة ولكنه لا يصل إليها أبدا.هذه واحدة من تناقضات زينون المستندة إلى اللانهاية، الفكرة التي خشيها اليونان وقتها لما تسببه من تناقضات.
ميز أرسطو بين مفهومين للانهاية، الأول هو اللانهاية الفعلية (actual infinity)، القبول بوجود واقعي للانهاية، مثل القبول بوجود واقعي للمجموعات اللانهائية مثل الأعداد الطبيعية. والمفهوم الآخر هو اللانهاية المحتملة (potential infinity) وهي التي تقوم على افتراض عد أو تقسيم متواصل ضمناً وليس واقعاً، كأن نستمر بإضافة واحد إلى مالانهاية،. رفض أرسطو المفهوم الواقعي للانهاية، فلا توجد لانهاية في عالمنا، مشيراً إلى عدم وجود عدد يمكن إضافته إلى آخر ويكون الناتج مساو للانهاية، مكتفياً بقبول اللانهاية المحتملة. فيمكن، ضمناً، العد بشكل لا نهائي، كما يمكن التقسيم بشكل لانهائي، وهو ما نجده في متناقضات زينون. لكن لا يمكن الوصول إلى هذا بشكل واقعي لأنه لا توجد لانهاية واقعية. تناقضات زينون كانت بسبب أخذ اللانهاية الفعلية على محمل الجد والقبول بواقعيتها، فيما كان الرد هو برفض هذا الخيار والاكتفاء بقبول لانهاية ضمنية وحسب.
استمر التمييز بين لانهاية واقعية ولانهاية ضمنية مع رفض الأولى والقبول بالثانية طويلاً، حتى القرن التاسع عشر. برغم وجود بعض الأصوات التي انحازت إلى إمكانية قبول اللانهاية الفعلية مثل غاليليو ولايبنتز، فإن الغالبية الساحقة (وفي مقدمتهم غاوس) لم ترَ إمكانية قبول بواقعية اللانهاية سواء في العلوم الطبيعة أو الرياضيات. وهكذا رُفضت المحاولات النادرة لتصور كون لانهائي، مثل نموذج جوردانو برونو، فبقيت فقط النظريات الطبيعية القائمة على أساس من كون منتهي في الزمان والمكان. وفي الرياضيات تمّ الاكتفاء باللانهاية المحتملة في حسابات التفاضل والتكامل وجموع السلاسل.
في النصف الثاني من القرن التاسع عشر تغيرت الصورة تماماً بفضل نظرية المجموعات لجورج كانتور، التي قدمت أساساً رياضياً لمفهوم اللانهاية وبهذا صارت اللانهاية الفعلية و بشكل نهائي مفهوم رياضي يتعذّر تجاوزه.
مفارقات اللانهاية: فندق هيلبرت
لنبدأ بفندق هيلبرت المسمى نسبة لديفيد هيلبرت.
إعلان
من الواضح أنه لن يكون ممكناً استضافة زائر جديد في أي فندق عادي يضم عدد منتهي من الغرف وجميعها ممتلئة، وذلك لعدم وجود غرفة شاغرة. فندق هليبرت، وعلى العكس من الفندق العادي، يحتوي عدد لانهائي من الغرف وجميعها مشغولة. هل يمكن لنا استضافة زائر جديد في فندق هيلبرت؟ الإجابة نعم.
يمثل الجدول أدناه فندق هيلبرت. يحوي السطر الأول أرقام الغرف (وقد ميزناها بسطر على الرقم)، فيما يحوي السطر الثاني أرقام الأشخاص الذين يشغولون هذه الغرف، فمثلأ الرقم 0 في السطر الأول يشير إلى الغرفة التي يشغلها الشخص الذي رقمه 0 في السطر الثاني.

لتأمين غرفة للزائر الجديد سنطلب من كل شخص أن ينتقل إلى الغرفة المجاورة له، أي من كل شخص له الرقم س أن ينتقل إلى الغرفة ذات الرقم س+1 كما في الجدولين في الأسفل. وكما نرى أصبحت الغرفة رقم 0 شاغرة وجاهزة لاستضافة الزائر الجديد.

ليس هذا فقط ما يمكن القيام به، بل يمكننا فعل ذات الأمر عدد لا منتهي من المرات. ففي فندق هيلبرت يمكن لنا دوماً إيجاد مكان لزائر إضافي وبشكل تكراري لعدد لامنتهي من الزوار.
لكن دعونا نجعل المسألة أكثر إثارة.هل يمكن لنا في فندق هيلبرت الممتلئ استضافة عدد لا منتهي من الزوار دفعة واحدة، وليس على مراحل؟ الإجابة أيضاً نعم، وذلك بالطلب من كل شخص س أن ينتقل إلى الغرفة ذات الرقم (2س+1).

وكما يظهر، فقد تمكنا من إيجاد عدد لانهائي من الغرف الفارغة في هذا الفندق، تستطيع مجموعة الزائرين اللامنتهية الانتقال إليها مباشرة. كذلك يمكن لنا القيام بهذا عدد لا منتهي من المرات.في فندق هليبرت يظهر أن الخبرة والحس غير كافيين للإجابة عما نطرحه من أسئلة، بل وحتى على تناقض مباشر مع مقتضى الحس وذلك لأننا نتعامل مع اللانهاية.
نظرية المجموعات
لنضع سؤالاً آخراً، أيّ المجموعتين أكبر، مجموعة الأعداد الطبيعية {0,1,2,3,….} أم مجموعة الأعداد الزوجية {2,4,6,….}؟
قبل الإجابة على هذا السؤال، دعونا نبدأ بتقديم بعض الأشياء حول نظرية المجموعات التي قدمها لنا كانتور، التي تعرف بنظرية المجموعات البسيطة naive set theory.
التعريف الأبسط والحدسي للمجموعة هو “أنها مجموعة الأشياء التي تملك خاصية مشتركة”[1]. وهكذا لدينا مجموعة الأعداد الطبيعية أو مجموعة لاعبي كرة القدم أو مجموعة الكواكب في مجرة درب التبانة وهلم. يتحدد حجم المجموعة بعدد عناصرها، فمجموعة كواكب المجموعة الشمسية هي ثمانية، ومجموعة فريق كرة القدم على أرض الملعب 11 وهكذا. ويعرف العدد الدال على حجم المجموعة بالعدد كاردينال (cardinal number). يمكن مقارنة أحجام المجموعات المنتهية بمقارنة عدد عناصرها الممثلة بالعدد كاردينال. ويمكن لهذا أن يتم عبر إيجاد تابع (علاقة) يربط بين عناصر المجموعتين، فإذا كان كل عنصر من المجموعة الأولى مرتبط بعنصر وحيد من عناصر المجموعة الثانية، فإن المجموعة الأولى أصغر أو مساوية للمجموعة الثانية. وإن كان كل عنصر من الأولى مرتبط بعنصر وحيد من الثانية، وكذلك كل عنصر من الثانية مرتبط بعنصر وحيد من الأولى، فإن المجموعتان متساويتان. وعليه فلإثبات تساوي مجموعتين، فإن كل ما علينا هو إيجاد علاقة تربط بين عناصر المجموعتين واحد إلى واحد.
لنعود إلى سؤالنا السابق، هل مجموعة الأعداد الطبيعية أكبر من مجموعة الأعداد الزوجية؟ سنلاحظ أنه من الممكن ترتيب عناصر المجموعتين بحيث يقابل كل عدد من الأولى عنصراً وحيداً من الثانية،
 وبالتالي فإن المجموعتان لهما نفس الحجم. هنا يمكن سريعاً –مرة أخرى- ملاحظة ما يعارض البداهة حين يتعلق الأمر بالمجموعات غير المنتهية. ففي المجموعات المنتهية، إن احتوت مجموعة أصلية مجموعة أخرى (مجموعة جزئية) ولم تكن المجموعة الجزئية هي نفسها المجموعة الأصلية، فإنها بالتالي أصغر من المجموعة الأصلية. لكن هذا لا يصدق في حالة المجموعات اللامنتهية. فمجموعة الأعداد الزوجية محتواة في مجموعة الأعداد الطبيعية وبرغم هذا فإن المجموعتان متساويتين في الحجم.
وبالتالي فإن المجموعتان لهما نفس الحجم. هنا يمكن سريعاً –مرة أخرى- ملاحظة ما يعارض البداهة حين يتعلق الأمر بالمجموعات غير المنتهية. ففي المجموعات المنتهية، إن احتوت مجموعة أصلية مجموعة أخرى (مجموعة جزئية) ولم تكن المجموعة الجزئية هي نفسها المجموعة الأصلية، فإنها بالتالي أصغر من المجموعة الأصلية. لكن هذا لا يصدق في حالة المجموعات اللامنتهية. فمجموعة الأعداد الزوجية محتواة في مجموعة الأعداد الطبيعية وبرغم هذا فإن المجموعتان متساويتين في الحجم.
يصدق هذا أيضاً على مجموعة الأعداد الكسرية، وهي مجموعة الأعداد التي تحوي كسوراً كل من بسطها ومقامها أعداداً طبيعية. مجموعة الأعداد الطبيعية محتواة في مجموعة الأعداد الكسرية، ولكن للمجموعتين نفس الحجم. يتمثل البرهان في إيجاد ترتيب (علاقة) يقابل فيها كل عدد من مجموعة الأعداد الطبيعية عدد من مجموعة الأعداد الكسرية، وهو ما يوضحه الجدول التالي.
نبدأ بالترتيب من السطر 0 حيت نضع بالترتيب أيضاً جميع الأعداد الكسرية التي بسطها مساوٍ للصفر، وفي السطر رقم واحد نرتب جميع الأعداد الكسرية التي بسطها واحد، وهكذا السطر رقم س جميع الأعداد الكسرية التي بسطها س.
ومن ثم نبدأ بشكل محوري من أقصى اليسار بإعطاء كل عدد كسري عدد طبيعي، بالأحمر، إذا كان يظهر لأول مرة. وإذا سبق وكان موجودا فلا نعطيه رقم (x)، وهكذا فإن كل الأعداد في السطر الأول ماعدا أولها لن تحسب لأنها جميعها مساوية للصفر.
وكما نرى يمكن لنا مقابلة كل عدد صحيح بعدد طبيعي، وبهذا يكون للمجموعتين نفس الحجم رغم أن الأعداد الطبيعية محتواة في مجموعة الأعداد الكسرية.

في نظرية المجموعات، تُعرف مجموعة بأنها قابلة للعد إذا كانت منتهية أو هناك علاقة واحد إلى واحد تربطها بمجموعة الأعداد الطبيعية. وهناك نظرية تقول أن مجموع مجموعتين قابلتين للعد هو مجموعة قابلة للعد. أي إذا كان لدينا مجموعة أ غير منتهية وقابلة للعد وتمت إضافتها إلى مجموعة ب غير منتهية وقابلة للعد، فإن الناتج مجموعة غير منتهية وقابلة للعد. وبما أن المجموعتين الأوليتين لهما حجم متساو ومساو لحجم مجموعة الأعداد الطبيعية، فإن الناتج بدوره مساو لحجم كل مجموعة من المجموعتين المشكلتين لها ومساو بدوره لمجموعة الأعداد الطبيعية.
بالإحالة إلى فندق هيلبرت، فإننا بعد أن أضفنا دفعة واحدة عدد لانهائي من الزوار الجدد، فإن حجم الفندق لم يزد بل بقي مساو لحجمه في المرة الأولى، وحتى لو أعدنا العملية لمرات كثيرة (لانهائي) لن يتغير حجم الفندق وسيبقى مساوياً لحجمه في المرة الأولى.
حسناً تبدو الأمور غريبة، لكن في النهاية نحن نتعامل مع اللانهاية واللانهاية واحدة. أبداً ليس هذا صحيحاً. لنأخذ مجموعة الأعداد الحقيقية فسنلاحظ أن هذه المجموعة أكبر من مجموعة الأعداد الطبيعية، أي أنه لا يوجد علاقة واحد إلى واحد تربطها مع مجموعة الأعداد الطبيعية، فهناك دوماً عدد حقيقي ليس له مقابل في مجموعة الأعداد الطبيعية. أي أن هناك مجموعة لا نهائية أكبر من مجموعة لانهائية أخرى.
لندفع بالأمور خطوة أخرى ولنسأل هل مجموعة الأعداد الحقيقية الموجودة بين الصفر والواحد أصغر أم مساوية لمجموعة الأعداد الحقيقية كلها؟ الواقع أنها مساوية بالحجم، فكل عنصر بين 0 والواحد يقابل عنصر من مجموعة الأعداد الحقيقية بين اللانهاية السالبة واللانهاية الموجبة، كما يظهر الشكل أدناه.
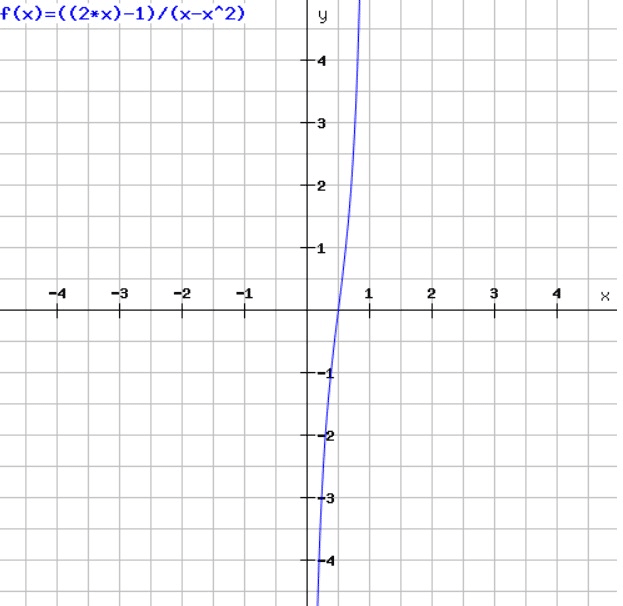
ويمكن البرهان على أن أي قطعة من مجموعة الأعداد الحقيقية لها نفس حجم مجموعة الأعداد الحقيقية نفسها، كما يظهر من الشكل أدناه، حيث يمكن وصل أي نقطة من أي مستقيم أفقي مع نقطة وحيدة من أي مستقيم أفقي آخر كما توضح الخطوط الواصلة بينهم.
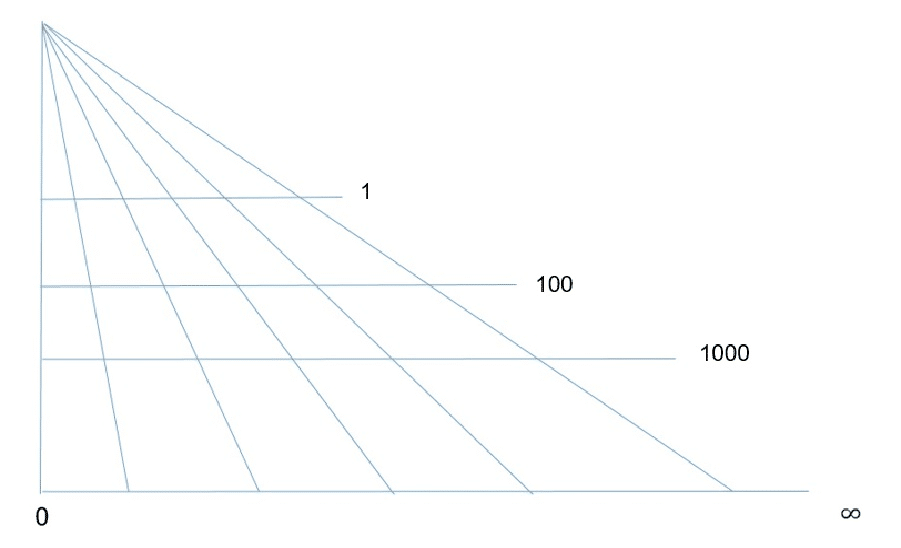
عبّر كانتور بشكل حاد عن هذه المفارقة في رسالته إلى ريتشارد ديدكيند بعد أن أظهر أن حجم مجموعة نقاط مربع مساوية لمجموعة النقاط الموجودة على أحد أضلاعه “أراه، لكني لا أصدقه”.
لنضيف نظرية أخرى وهي أن مجموعة (قوة مجموعة) هي أكبر من المجموعة نفسها. ومجموعة (قوة مجموعة) هي المجموعة المشكلة من كل المجموعات الجزئية للمجموعة. مثلا ليكن لدينا مجموعة ع من عنصرين وحسب {0,1} فإن مجموعة قوة المجموعة هي المجموعة التالية {{},{0},{1},{0,1}}، ولنرمز للأخيرة بالرمز ق(ع). وبالتالي ق(ع) > ع.
وعليه نحن ليس لدينا فقط مجموعة لانهائية (مجموعة الأعداد الصحيحة) أكبر من مجموعة لانهائية (مجموعة الأعداد الطبيعية)، بل لدينا عدد لانهائي من المجموعات اللانهائية التي كل منها أكبر من سابقتها بشكل لا نهائي، فلتكن ع مجموعة الأعداد الحقيقية وعندها
ع < ق(ع) < ق(ق(ع)) < ق(ق(ق(ع))) < ….
وبهذا الشكل يمكن البرهان على امتناع وجود المجموعة الشاملة، المجموعة التي تضم كل شيء، لأنه يمكن دوماً، وبشكل لانهائي، بناء مجموعة أكبر.
ومن أجل التعامل مع هذه الأعداد اللامتناهية والمختلفة أدخل كانتور مفهوم العدد غير المنتهي (transfinite number)، وهو العدد الأكبر من كل الأعداد المنتهية. والعدد له بعدين (أو معنين)، فهو يدل إما على موقع العنصر في المجموعة، ويسمى عدد الترتيب (ordinal number)، فمثلاً العدد خمس هو العنصر ذو الترتيب الخامس في مجموعة الأعداد الطبيعية. أو يدل على حجم المجموعة ويسمى بالعدد كاردينال كما سبق ورأينا. وفيما يخص الأعداد غير المنتهية، فهي قد تدل على أعداد الترتيب، أي الأعداد غير المنتهية الأكبر من كل الأعداد المنتهية، وقد سمى كانتور أصغر عدد لامنتهي أوميغا ω، وبفضل هذه الملاحظة المقدمة حول الأعداد غير المنتهية يمكن لنا القيام بالعمليات الرياضية باستخدامها، مثل إضافة واحد إلى أوميغا أو غيرها من العمليات.وبهذا يكون أوميغا أول درجة في سلسلة الأعداد غير المنتهية والمستمرة أيضاً بشكل غير منتهي. كذلك يدل العدد، في معناه الثاني، على الحجم الخاص بالمجموعة (العدد كاردينال)، وعندها يكون أصغر عدد لامنتهي هو ألفا_صفر وهو حجم مجموعة الأعداد الطبيعية.
لنعيد ترتيب بعض الأفكار: يمكن مقارنة أحجام المجموعات اللانهائية ببعضها البعض، وسنرى أن هناك مجموعات أكبر من أخرى، وبالتالي فإن هناك لانهاية أكبر من أخرى وهكذا بشكل لانهائي.عند التعامل مع المجموعات اللامنتهية فإن عدد من الخبرات التي نعتمدها لن تكون صحيحة، مثل أن مجموعة محتواة في أخرى لن تكون بالضرورة أصغر حجماً منها. كذلك عند إضافة مجموعات لانهائية لبعضها البعض، فإن الناتج ليس بالضرورة مجموعة أكبر من سابقاتها.
كانتور، الذي كانت لديه ميول لاهوتية ودينية قوية، سيرى أن مفهوم اللانهاية الفعلية يفترض ضمناً وبشكل ضروري مفهوماً آخراً للانهاية وهو ما يسميه باللانهاية المطلقة، التي توجد في مجال آخر من الوجود الأعلى والأكثر كمالاً. هناك، في هذا المستوى الأعلى، تتجلى اللانهاية بشكل واقعي وحقيقي وعندها تصير مطلقة. وبفضل هذا المستوى الأعلى التي تتحقق فيه اللانهاية المطلقة، يمكن أن تظهر اللانهاية الفعلية في عالمنا، حيث يمكن للمرء أن يدركها باعتبارها كائن رياضي مجرد، كأعداد لامنتهية. وبهذا فإن شيئاً من خصائص اللانهاية المطلقة يظهر في خصائص اللانهاية الفعلية التي تتناولها نظرية المجموعات.
فاللانهاية الفعلية، بوصفها كائن رياضي مجرد،تظهر في نظرية المجموعات بفضل وجودها في مستوى أعلى للتحقق الكامل لها، لانهاية مطلقة. هذه اللانهاية المطلقة ليست في النهاية إلا الله كما أعتقد كانتور الذي اتجه في أواخر سنين حياته إلى محاولة استخراج ما يترتب على نظريته في المجموعات من نتائج دينية ولاهوتية.
اللانهاية والمطلق
انطلاقاً من فكرة كانتور عن اللانهاية المطلقة ومكافئتها مع الله يمكن مقاطعة نقاش اللانهاية مع المطلق. وقد كان نقاش اللانهاية خلال القرون الوسطى مرتبط مباشرة بمسألة المطلق وبمضامين لاهوتية. ولنأخذ مثلاً على التناقض الخاص بمفهوم المطلق (الله) للتدليل على التقاطع بين مفارقات اللانهاية والمطلق.
السؤال هو إن كان الله قادرًا على كل شيء (مطلق القدرة) فهل يمكن له أن يخلق حجراً لا يستطيع هو حمله؟ إذا قلنا أنه قادر على خلق مثل هذا الحجر، فهو غير قادر على حمله (تناقض). وإذا قلنا أنه بالضرورة قادر على حمل كل حجر، فهو بالتالي غير قادر على خلق حجر بالمواصفات المطلوبة (تناقض).
لنزح البعد الديني للمسألة، ولننظر إلى المثال مرة أخرى فسنجده أنه يطرح إشكالاً حول فكرة المطلق نفسها، وهي أن تعيّن (إضفاء سمة واقعية) للمطلق يؤدي إلى تناقض يتمثل بإمكانية إضافة خطوة إلى هذا المطلق نفسه، أن يذهب خطوة إضافية إلى مابعد الحد. المسألة موازية للتناقض الناشئ عن قبول وجود واقعي لمجموعة الأعداد الطبيعية (تناقض بورالي-فورتي)، فليس هناك حداً أعلى طالما نحن قادرون دوماً على إضافة واحد. وهكذا أيضاً بالنسبة لمطلق قادر على خلق كل شيء، فما علينا إلا أن نضيف خطوة، هل هو قادر على خلق ما لا يمكن حمله؟ هكذا نجد أنفسنا في دائرة لن نخرج منها (طبعاً اللاهوتيون اهتموا بتفكيك السؤال أكثر من محاولة الإجابة عنه).
بلور التقليد الإسماني، وبشكل خاص أعمال وليم أوكهام، تصور الله المطلق القدرة. فالله، بحسب هذا التصور، يستطيع أن يفعل أي شيء انطلاقاً من حرية إرادته. وبهذا لا يمكن لأي شيء أن يحد من قدرته أو حرية إرادته، حتى لو كان هذا الشيء قيم عقلية أو أخلاقية (مثل الخير والصدق وغيرها) أو القانون. فالقيم نفسها قيم لأن الله اختارها، ويستطيع أن يغيرها وقتما يشاء. فالخير ليس خيراً بذاته، بل لأن الله اختاره. هكذا، يمكن لله أن يغير وعده للمؤمنين بإعطائهم الجنة وللعاصين بعقابهم في جهنم بأن يفعل العكس تماماً، فيرسل العصاة الكفرة إلى الجنة والمؤمنين إلى جهنم. إلزام الله بأن يصدق بوعده، لأن الصدق خير والله لا يكذب، يعني أن هناك قيم ومعايير ملزمة بذاتها (خير في ذاتها، موجبة في ذاتها) تلزم الله في سلوكه (لم يعد الله مطلق القدرة)، وعليه فلا حاجة لنا لله الذي لم يعد مطلقاً، فهو بدوره خاضع وملزم بالقانون والمعيار والقيمة[2].الله المطلق القدرة، الذي صار بإمكانه أن يفعل أي شيء مثل أن يعيد غداً خلق العالم من جديد أو يغير قوانينه وحتى أن يخدعنا، أمسى أشبه بالشيطان منه بالله ومدمراً بهذا الشكل نسق المعقولية في العالم. بالتأكيد لم يذهب أوكام ومناصروه إلى هذا المدى، فحاولوا تجاوز هذا الإحراج المتضمن في فكرة الإله مطلق القدرة من خلال التمييز بين القدرة المتعينة والقدرة المطلقة، وهو أمر يشبه التمييز بين اللانهاية الفعلية واللانهاية المحتملة، وهو تمييز كان محرجاً لتعسُرتبريره والحفاظ عليه من داخل النسق الإسماني نفسه[3].
تتعلق المعضلة، وبمعزل عن جانبها اللاهوتي، بالتناقض الناشئ عن مفهوم المطلق نفسه، بنفس الطريقة التي نشهدها مع التناقضات التي يحملها مفهوم اللانهاية ومحاولة تعيينه واقعياً. هناك دوماً ما هو وراء، ويمكن لنا حتى اللانهاية أن نذهب في هذا الماوراء، بحيث أن أية محاولة لتعيينه ستؤدي إلى تناقض.
خاتمة
مفهوم اللانهاية مفهوم إشكالي وباب للتناقضات والمفارقات، سواء في نسخته الرياضية أو في نسخته المفهومية (المطلق)، ولهذا تم استبعاد تحققه الواقعي من الرياضيات والعلوم لمدى طويل، حتى نجح كانتور بفضل نظريته في المجموعات في تأمين أساس رياضي للمفهوم، “وهكذا، وبفضل التعاون الجبار بين كانتور وديدكيند وفريجة أصبحت اللانهاية ملكاً تتمع بانتصار عظيم” كما سيقول ديفيد هيلبرت (حول اللانهاية، 1926). لكن هذا لم يعني أن المفارقات تم تجاوزها، بل بقيت في تناقضات ومصادمة للحس والخبرة.
هنا يمكن لنا طرح عدد من الأسئلة التي سنتركها مفتوحة للتفكير. كما رأينا أن السؤال الأول حول معنى القبول بواقعية اللانهاية الفعلية؟ إن القبول بواقعيتها ككائن رياضي مجرد، يطرح علينا السؤال حول طبيعة وجود الكائنات الرياضية المجردة وهي مسألة ناقشناها في مقال سابق[4]. لكن فيما يتعلق باللانهاية تصبح المسألة كما يبدو أشد تعقيداً لما تطرحه من مفارقات. بل إن سيزار بورالي-فورتي (Cesare Burali-Forti) برهن أن القبول بوجود “مجموعة كل الأعداد الطبيعة/كل أعداد الترتيب” سيؤدي إلى تناقض، وهو ما يُعرف بتناقض بورالي-فورتي.
هل قبول واقعية اللانهايات الفعلية يُلزمنا بقبول واقعية مستوى آخر من الواقع مخصص للكائنات المجردة؟ وما تفسير التناقضات والمفارقات التي تنشأ عن قبول اللانهاية الفعلية؟ هل هي متعلقة بطريقة إدراكنا؟ هل هناك مستوى أعلى، كما افترض كانتور نفسه فيما يخص اللانهاية المطلقة، يحدد خصائص اللانهايات الفعلية وهناك ينتفي التناقض الناشئ عن طبيعة إدراكنا نحن للانهاية الفعلية؟.
في المقابل هناك من الرياضيين من اعترض على عمل كانتور، وفي مقدمهم ليوبولد كرونكر (Leopold Kronecker) الذي يُنسب له قوله “لا أعلم ما الذي يطغى في نظرية كانتور – الفلسفة أم اللاهوت، لكن الشيء الذي أنا أكيد منه، أنه لا يوجد هنا شيء من الرياضيات”. ومن الذين ما يزالون يعترضون على القبول باللانهاية الفعلية أنصار المذهب الحدسي، الذين يرون أن الكائنات الرياضية هي مجرد تصورات عقلية، وعليه فهم يشيرون إلى أن ما ندركه من تناقضات ينبع أساساً من طبيعة تصوراتنا، ولهذا مثلما حصلت محاولة لتقديم نظام تبديهات لا يتطلب القبول بفكرة اللانهاية الفعلية ويكتفي باللانهاية المحتملة.
سؤال آخر يُطرح علينا، كيف لكائن منتهي في الزمان والمكان مثل الإنسان في وجود منتهي ككوننا، فهناك عدد منتهي من الأجسام الأولية، أن يفكر بمفهوم مثل اللانهاية؟ لا يبدو أن هناك ما يساعد على إيضاح قدرتنا على تصور اللانهاية انطلاقاً من الخبرة والتجربة. وهنا يمكن لنا العودة إلى أرسطو ونقده لمفهوم اللانهاية الفعلية، ففي النهاية لا يوجد عدد نضيفه لآخر يعطينا لانهاية. أما تخيل مفهوم اللانهاية الفعلية انطلاقاً من اللانهاية المحتملة فهو أيضاً يفترض إشكالاً يتمثل في دائرية المفهوم. فأن يكون تصورنا للانهاية ناتج عن إمكانية العد بشكل لا منتهي، يعني أننا نضع اللانهاية أساساً في التعريف (العد بشكل لانهائي). للوصول إلى اللانهاية نحتاج أصلاً قدرة على تصور قدرة القيام بالأمر بشكل لانهائي. إننا ندور في حلقة. والأسوأ أن هذه القدرة في نفسها قدرة متخيلة، حتى لو تخيلت الكون بأكمله كحاسوب فلن يكون بإمكانه العد إلى اللانهاية.
[1]هذا التعريف هو الأساس في نظريات المجموعات الساذجة في نسختها الأولى وهو متناقض كما بين لاحقاً كل من تسيلمرو وراسل، ولكنه كاف لنا هنا. [2]العلاقة بين الله والقانون ما تزال موضوع راهن ومثار جدل، وهو ما سنتاوله في مقال آخر. [3]من أجل مراجعة أوسع يمكن العودة إلى الجزء كتاب "الجذور اللاهوتية للحداثة" لمايكل ألان غيليسبي، وترجمة قبصل الفرهود، المنشور على موقع مجلة حكمة. https://hekmah.org/الجذور-اللاهوتية-للحداثة-مايكل-آلين-غ/ [4]https://elmahatta.com/فلسفة-الرياضيات-الأسئلة-والمدراس/
إعلان
