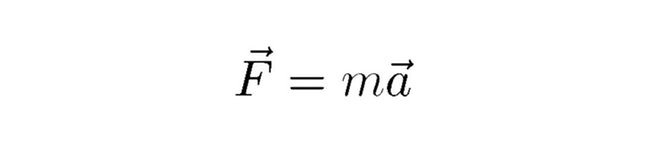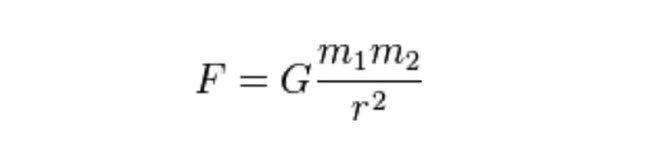مجموعة من المعادلات الفيزيائية غيرت مجرى التاريخ

لقد شهدت القرون القليلة الماضية بعض الأحداث المحورية التي منحت البشرية اختراعات عظيمة غيرت مجرى التاريخ وكانت كلها بفضل الفيزياء، إذ تعتبر المعادلات الفيزيائية شكلًا من أشكال السحر الذي يفسر لنا الماضي بأسراره التي ظلت مجهولةً لقرون عديدة كـ”مُذّنب هالي” الذي ظلّ يزور كوكبنا كل 76 عامًا، كما تسمح لنا أيضًا بالتنبؤ بالمستقبل، ووصلت بذلك بعيدًا إلى درجة أننا نعرف الآن المصير النهائي والمأسوي للكون.
وتضع أحيانًا حدودًا للممكن كما هو الحال مع أقصى كفاءة عملية يمكن أن يصل لها المحرك، كما قد تكشف لنا عن إمكانات لم نكن يومًا لنتخيلها، مثل الطاقة الموجودة داخل الذرة.
وفي بعض الأحيان على مر القرون الماضية، منحت معادلة جديدة الجيل القادم أداة سحرية مكنته من تغيير مجرى التاريخ، وهنا بعض أهم تلك المعادلات:
1- قانون نيوتن الثاني للحركة (1687)![]()
ما الذي تخبرنا به هذه المعادلة؟
تنص على أن القوة تساوي حاصل ضرب كتلة الجسم في العجلة التي يتحرك بها، وبمعنى آخر أنّه من الأسهل أن تدفع عربة تسوق فارغة، على أن تدفع أُخرى ممتلئة.
ماذا نتعلم من هذه المعادلة؟
بالإضافة لقانوني نيوتن الأول والثالث للحركة (الأول يقول أننا نحتاج إلى قوة لنحرك جسم ساكن، والثالث يقول أن لكل فعل رد فعل مساوي له في المقدار ومضاد في الاتجاه) شكلّت هذه المعادلات، رغم شعورنا ببدهيتها، الأساس الذي قامت عليه الميكانيكا الكلاسيكية.
إعلان
فالقانون الثاني سمح للمهندسين والفيزيائيين بحساب مقدار أي قوة نحتاج حسابها، فعلى سبيل المثال، مقدار وزنك (بالنيوتن) يساوي حاصل ضرب مقدار كتلتك (بالكيلو جرام) ومقدار عجلة الجاذبية (والذي يساوي تقريبًا 10 م/ ث^2).
وبذلك إذا كانت كتلتك 60 كجم، فإنك تؤثر على الأرض بقوة 600 نيوتن.
هل لها تطبيق عملي؟
كان لهذه المعادلة الفضل في الوصول إلى العصر الميكانيكي الذي عرفت فيه أوروبا المحرك فتغير فيها شكل الحياة والصناعة، حتى الحروب عرفت أسلحة مختلفة، فقد تم استخدام تلك المعادلات في كل الحسابات التي تضمنت استخدام قوة للتسبب في حركة.
فهي تخبرك بمدى قوة المحرك الذي نحتاجه لتحريك سيارة، أو مقدار قوة الرفع التي تحتاجها الطائرة لكي تحلق إلى الأعلى، أو قوة الدفع التي نحتاجها لينطلق الصاروخ، وحتى المدافع استخدمتها لحساب دفع وتوجيه القذائف.

2- قانون الجذب العام لنيوتن (1687)![]()
ما الذي تخبرنا به هذه المعادلة؟
أي جسمين في الفضاء يجذب كل منهما الآخر بقوة تتناسب طرديًا مع حاصل ضرب كتلتيهما، لكنها تقل بسرعة كلما ابتعد كل منهما عن الآخر. وبعبارة أخرى، نحن ملتصقون بسطح الأرض لأن كوكبنا كبير نسبيًا نتيجة لعظم الكتلة الموجودة فيه.
ماذا نتعلم من هذه المعادلة؟
لقرون انقسم العالم إلى جزأين لا يوجد ما يربطهما، حتى جاء نيوتن بقانونه للجذب العام فربط الأرض والسماء، فنفس القوة التي تسبب سقوط التفاحة من على الشجرة هي التي تجعل القمر يدور حول الأرض.
لقد أعطانا نيوتن أول اتصال مباشر بين كل شيء في الحياة، لقد منحنا ما نفسر به كل ما يتحرك على الأرض أو في السماوات.
هل لها تطبيق عملي؟
لمدة طويلة لم تُستخدم إلا في حساب مدارات الكواكب، حتى عصر الفضاء خلال الحرب الباردة في خمسينيات وستينيات القرن الماضي حيث تم استخدامها أخيرًا عمليًا في إرسال الأقمار الصناعية لتدور حول الأرض، وإرسال رواد الفضاء إلى القمر.
أحد أوجه فشل هذه المعادلة والتي اعترف بها نيوتن نفسه أنّها لا تعطي تفسير لسبب الجاذبية، وقد لزمنا قرابة 230 عامًا حتى جاء آينشتاين بنظريته النسبية العامة، فقدم لنا تفسيرًا وهو أنّ الجاذبية ناتج للانحناء الذي تشكله الأجسام في نسيج الزمكان.
ومع ذلك نحن لا نستخدم النسبية العامة في حساباتنا إلا في الحالات المتطرفة عندما تكون الجاذبية قوية جدًا مثل الحسابات داخل الثقوب السوداء، أو عندما نحتاج دقة عالية مثل حسابات الـ GPS للأقمار الصناعية.
فمعادلة نيوتن والتي تبلغ قرابة 330 عامًا ما زالت مفيدة إلى الآن، وأكثر استخدامًا لما تتسم به من بساطة وسهولة.
3- القانون الثاني للديناميكا الحرارية (1824)

ما الذي تخبرنا به هذه المعادلة؟
الإنتروبي (وهي مقياس للعشوائية) في زيادة مستمرة.
فلا جدوي من البكاء على اللبن المسكوب، فالعشوائية والفوضى أمر لا مفر منه في عالمنا ولا يمكن عكسهم.
ماذا نتعلم من هذه المعادلة؟
أثناء محاولات الفيزيائي الفرنسي كارنوت لتحليل المحرك البخاري في القرن التاسع عشر، توصل إلى أحد أكثر المعادلات الفيزيائية عُمقًا في كل العلوم.
حيث تخبرنا بأن بعض العمليات لا يمكن عكسها، وبعضها قد يكون مسؤولًا عن اتجاه الزمن للأمام دائمًا، وفي إحدى أبسط صورها تخبرنا بأن الحرارة تنتقل من الأجسام ذات الحرارة الأعلى إلى الأقل.
ويمكن تطبيقها أيضًا على أوسع النطاقات، فالبعض طبقها على الكون فعرّفتنا بالمصير النهائي له وسيكون عبارة عن “موت حراري”، حيث ستنطفئ كل النجوم ولن يتبقى إلا الحرارة المُهدرة.
والبعض استخدمه للرجوع عبر الزمن وصولًا إلى نقطة التفرد “singularity” حيث بداية الكون، وهي بمثابة لحظة الإنتروبي الصفرية أو النظام المطلق عند بداية الانفجار العظيم.
هل لها تطبيق عملي؟
كان هذا القانون مهمًا لتطور التكنولوجيا خلال الثورة الصناعية، بداية من المحرك البخاري مرورًا بمحركات الاحتراق الداخلي إلى الثلاجات والهندسة الكيميائية.
4- معادلة ماكسويل- فاراداي (1831-1865)
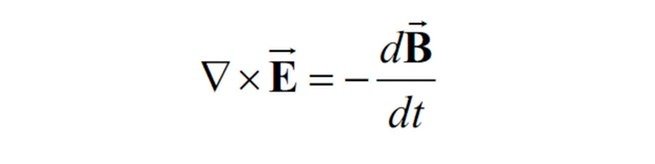
ما الذي تخبرنا به؟
يمكنك توليد مجال كهربي متغير (الجانب الأيسر من المعادلة) باستخدام مجال مغناطيسي متغير (الجانب الأيمن من المعادلة) والعكس، وبذلك تكون الكهربية والمغناطيسية متصلتين ببعضهما البعض.
ماذا نتعلم من هذه المعادلة؟
اكتشف مايكل فاراداي في عام 1831 الصلة بين المغناطيسية والكهربية، عندما وجد مجال مغناطيسي متغير ينتج عنه تيار كهربي في سلك قريب.
فيما بعد استطاع ماكسويل تعميم ملاحظة فاراداي كأحد معادلاته الأربعة الأساسية في الكهرومغناطيسية.
هل لها تطبيق عملي؟
هذه هي المعادلة التي تمد العالم بالطاقة، فأغلب المولدات الكهربية سواء توربينات الرياح أو محطات الفحم أو السدود الكهرومائية تعمل عن طريق تحويل الطاقة المختزنة في البخار أو الماء إلى طاقة ميكانيكية دورانية خلال مجال مغناطيسي.
وإذا أردنا الحصول على موتور كهربي نقوم فقط بعكس هذه العملية.
ولا زالت تُستخدم حتى اليوم تقريبًا في كل التطبيقات المتعلقة بالهندسة الكهربائية وتطبيقات الاتصالات والبصريات.
5- معادلة آينشتاين لتكافؤ الكتلة والطاقة (1905)
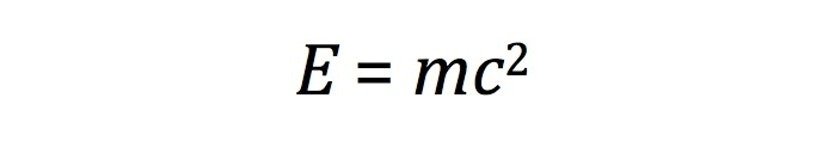
ما الذي تخبرنا به؟
الطاقة تساوي حاصل ضرب الكتلة في مربع سرعة الضوء، وبذلك الكتلة ما هي إلا شكل من أشكال الطاقة المكثفة بشدة.
ماذا نتعلم من هذه المعادلة؟
نظرًا لأن الثابت في هذه المعادلة رقم مهول جدًا (مربع سرعة الضوء ويساوي 10^9)، يمكن إطلاق كم هائل من الطاقة نتيجة تحويل جزء صغير جدًا فقط من الكتلة.
هل لها تطبيق عملي؟
أعطت معادلة آينشتاين الأكثر شهرة تلميح بأننا نستطيع الحصول على كم هائل من الطاقة من خلال الانشطار النووي، وذلك عندما تنشطر نواة كبيرة غير مستقرة إلى نواة أصغر مع وجود فرق في الكتلة يتحول إلى طاقة هائلة.
والقنبلة الذرية “Fat Man” التي أُلقيت على ناجازاكي في 9 أغسطس من عام 1945 خلال الحرب العالمية الثانية حولت واحد جرام فقط من الكتلة إلى طاقة، ولكنها أنتجت انفجار يعادل 20 ألف طن من مادة الـ “TNT” شديدة الإنفجار.
آينشتاين نفسه وقّع على خطاب إلى الرئيس الأمريكي وقتها “فرانكلين روزفلت” يوصيه بتطوير القنبلة الذرية، وهو قرار اعتبره لاحقًا “أحد أعظم الأخطاء” التي ارتكبها في حياته.
6- معادلة الدالة الموجية عند شرودنجر (1925)
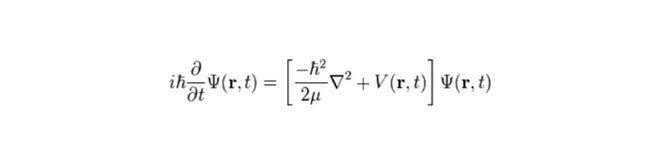
ما الذي تخبرنا به؟
تصف كيف يمكن أن نحسب تغير الدالة الموجية للجسيم عن طريق طاقة حركته (نتيجة حركة الجسيم) وطاقة الوضع (نتيجة التفاعلات عليه)، وهي تناظر معادلة نيوتن “F=ma” لكن في عالم الكم.
ماذا نتعلم من هذه المعادلة؟
عندما وضع شرودنجر معادلته عام 1925، جعل ميكانيكا الكم تقف على أرض صلبة من خلال السماح للفيزيائيين بحساب كيفية تحرك الجسيمات الكمومية وكيفية تفاعلها.
قد تبدو معادلة شرودنجر غريبة بعض الشيء لاستخدامه الرياضيات التي تصف الموجات، ولكن الجسيمات تحت الذرية لها طبيعة مزدوجة فهي بجانب طبيعتها كجسيمات تتصرف كموجات ايضًا، فهي لا تتصرف ككرات البلياردو.
هل لها تطبيق عملي؟
في إحدى أبسط صورها، تصف هيكل الذرة، بدايًة من ترتيب الإلكترونات حول النواة، حتى جميع الترابطات الكيميائية.
وبشكل عام، يتم استخدامها في العديد من الحسابات في ميكانيكا الكم، وهو أساس العديد من التقنيات الحديثة من أشعة الليزر حتى الترانزيستورات والتي هي أساس الكومبيوتر وجميع الأجهزة الإلكترونية الحالية.
كما أن التطور المستقبلي لأجهزة الكمبيوتر الكوانتية معتمد على ميكانيكا الكم، وهي ذات قوة وكفاءة أعلى بمراحل عديدة من الأجهزة الحالية.
إعلان