ما لن تعرفه عن الرياضيات

فكّرتُ كثيرًا في جعل العنوان “ما لم تعرفه عن الرياضيات” باعتبار أنّك ستعرف بمجرّد قراءة هذا المقال، لكنّني تذكرتُ أنّ الكثيرين لا يعرفون أيّ شيء عن الرياضيات، وبالتالي سيحتاج الأمر ربما لمجلّداتٍ لذكر ما لا يعرفونه. لهذا فكّرت في جعل المقال مُفارقة منطقية في ما لن تعرفه عن الرياضيات، والغرض هنا ليس المفارقة حقًا وإنَّما الإيجاز، والمقصود بما لن تعرفه سوى من خلال المقال أو الكتاب نفسه الذى سأذكر اسمه فى المصادر، والسبب هو نُدرة التحدُّث عن الرياضيات كعلمٍ بسيط يمكن لأي كان أن يفهمه لأنّه يعتمد بالأساس على التتابع فما تأخذه الآن سيفيدك لاحقًا وما تأخذه لاحقًا سيفيدك فيما بعد وهكذا. وهو من أكثر العلوم اتصالًا كالسلم فلا يمكنك الوصول لنهاية السلم بدون أن تصعد وتتذكر أين كانت خطواتك فوق كل دَرجة على حدى وأين يجب أن تضعها في الدرجةِ القادمة.

إنّ ما سيتم ذكره هنا على الأرجح أشياء منطقية أكثر منها رياضيات، فالرياضيات أساسًا قائم على المنطق الذى نعبر عنه بالأرقام لهذا قد تكون دارسًا لهذا العلم لكن لا زال بإمكان المقال أن يمتعك، وقد تكون هاويًا أو حتى شخص لا يعرف أى شئ عن الرياضيات ويرغب بالتجربة.

ولهذه الفئة الأخيرة أكتب..

إنّنا صِغارًا حين نُفكّر في الرياضيات نفكّر فيه على أنّه علم جافّ وصارم جدًا، وأنّ واحد + واحد = اثنان ولا يمكن بأى حال أن يساوي ثلاثة، وحتى لو رأيتها من أي اتجاه سيظل الناتج اثنان رغم أنفك وأنفي وأنف مؤلف الكتاب.

لكنك حين تتقدم فى دراسة هذا النوع من العلوم تكتشف أنه ربما لا يكون الرياضيات صارم جدًا، لأن بعض الأمور لا نعرف لها حلولًا صارمة أو دقيقة ولهذا نضطر للجوء إلى التقريب، فعلى سبيل المثال قد تحصل على ناتج 200 لمسألة ما، وأحصل أنا على ناتج 250، ويكون الناتج الصحيح شيئًا آخر لكننا نعتبره كله صحيحًا ما دام لن يؤثر في النتائج بشكلٍ ملحوظ.

إن شيئًا كهذا لا تعتاد عليه بسهولة لأنه ببساطة يجعل الرياضيات تخسر ميّزتها الواضحة بالنسبة لك “الصارمة الجافة النظيفة” ولكنك لو اخترت ألّا تسلك طريق التقريب فستخسر الكثير من الأمور المفيدة التى نتوصل إليها عن طريق التقريب، فالعديد من النظريات والحلول الرياضيّة قائِمة بشكل أساسي على التقريب، وهناك بعض المعادلات التى لم يتم التوصل إلى حلول دقيقة لها إلى الآن، ولكنك بالتقريب تَحصُل على نتائِج أقرب ما تكون إلى الصحة وأنت تعلم أن الحصول على شئ غير كامل أفضل من لا شيء على الإطلاق.

ادعني آخذك فى رحلة خلال هذا العلم المليء بالأمور الطريفة والشيقة، ولنجعل الأمر أكثر متعة دعنا نتخيل هذا المقال كقطار، وكل موضوع نتحدث به هو محطة نمكث فيها قليلًا ثم نتركها..

الآن اجلس من فضلك لأن القِطار على وشك أن يتحرك..

المحطة الأولى : القواعد البسيطة والتقريب ..

جميعنا نعلم أنّ القواعد البسيطة قد تتحول إلى كوارث إن لم تكن ليّنة، وكمثال بسيط لو أخبرتك أمك ألا تتحدث أبدًا والطعام فى فمك، فهذه قاعدة صارِمة وأي تجاوز لها سيؤدي إلى نتائج لا تُحمد عُقباها، وأنت تعلم ما أعنيه فشبشب الحجة مؤلم حقًا، خصوصًا حين يتم رميه بسرعة 200 م فى الثانية.

لكن لنفترض أنه لسببٍ ما عَلِق الطعام بحلقك ولم تستطع التنفس، هنا سيكون عليك كسر القاعدة وربما كسر زجاج المنضدة لتجعلهم ينتبهون للأمر قبل أن يتوفاك الله، وكذلك قد تتحول المتسلسلة ذات القاعدة البسيطة إلى كارثة رقمية لولا استخدام التقريب.

مثال بسيط :

لنفترض أنّ لدينا متسلسلة هى عبارة عن a1 ,a2 ,a3,a4، حيث a1 لها قيمة وهي الواحد الصحيح.

جميل، والآن القاعدة بسيطة كل رقم هو مجموع كل من الرقم الذى يسبقه وجذر الرقم الذى يسبقه.

إن كنت تلاحظ فالمتسلسلة تتحول إلى كارثة رقميّة وسيظل طولها يزداد حتى لا يعود بإمكانك كتابة قيمة الرقم الواحد فى سطر واحد لكن هل يعنى هذا أنه لا يمكننا فهم هذه المتتابعة؟

بالطبع لا فالحل السحري دائِمًا التقريب..

فمثلًا، بدلًا من إخبارك أن a4 قيمتها تلك القيمة المكتوبة أعلاه، بإمكاني إخبارك أن a4 قيمتها تقريبًا 5.26 ولن يضر ذلك من فهمك لقيمة a4 كثيرًا، فبإمكانك فهم رقم 5.26 لأنه منته بينما قيمة a4 الحقيقية غير منتهية.

الآن ما نحتاج إليه هو قاعدة عامة تصف an ولأنّنا نعلم بالتجربة أن an يصعُب وصفها بشكلٍ دقيق فإنّنا نعلم مسبقًا أن القاعدة ستكون قاعدة تقريبية وسيكون بها نسبة من الخطأ، أما عن الطريقة التى سنوجِد بها هذه الصيغة فلنفترض أن معنا نوعًا من العُصي السحريّة نضعُها فوق المتسلسلة، فتنتج لنا صيغة بإمكانِها إيجاد قيم تقريبية للan حيث الn = 1,2,3,4,5..

الآن العصا تقول أن الصيغة لل an هي n^2 / 4

أي أن الصيغة لل (a(n+1 هى n+1)^2 / 4)

والآن، بِفك القوس التربيعي وطريقة فكه وهي كالآتي العنصر الأول تربيع + العنصر الثاني تربيع + الأول في الثاني في اثنين، لكنك لا تحتاج لإجهاد عقلك بالأمر فبإمكانك أن تأخذ حديثي موضِعَ ثقة، فأنا فقط أذكرها لأولئك المتشككين فى نهاية المقطورة.

لازلت تذكر أننا فى القطار صحيح؟

تووووت توووووت نعم اقتربنا من مغادرة المحطة الأولى فاستعدوا..

الآن بالعودة إلى الصيغة نجد أنها تساوي n^2 +2n+1) /4)

وبتوزيع القسمة نصل فى النهاية إلى n^2 / 4 + n/2 + 1/4

لكننا نستطيع كتابتها رياضيًا بطريقة أخرى ولمرة أخيرة عليك أن تأخذ حديثي موضع ثقة عندما أقول لك أن تلك الصيغة تساوى تمامًا هذه:

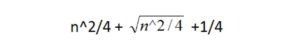وها هي القاعدة تظهر لنا فهذا يعنى أن (a(n+1  لها قيمة تساوى الرقم الذى يسبقها + جذر الرقم الذى يسبقها + 1/4

وفى أرقام كبيرة من المتسلسلة سيكون ال1/4 رقمًا صغيرًا جدًا، بحيث أنه تصبح بشكلٍ ما نسبة الخطأ معقولة بل وصغيرة أيضًا و يمكن القبول بها.

ولهذا نستطيع أن نقول في النهاية أنّه على الرغم من تعقيد تلك المتسلسلة إن فكرت في أخذِها على النحو الدقيق، إلا أنّها تصبح أبسط بكثير لو استخدمت الحل السحري التقريب.

الآن، أنا أعلم أنَّك مرهق وتريد الاستمتاع بالطريق لهذا سنترك الموضوع الآخر لمحطة أخرى وربما نتحدث به خلال الطريق من يدري..

*الاعداد غير المنتهية: هى أعداد ليس لها تمثيل عشري منته مثل جذر2.

المصادر: كتاب الرياضيات مقدمة قصيرة جدًا، الفصل السابع.