أجملُ معادلات العلمِ

المعادلات الرياضية ليست فقط مُفيدة -كثير منها جميل جدًّا. ويعترف العديدُ من العلماء بأنّهم غالبًا ما يكونون مُغرمين بصِيَغٍ خاصّة ليس فقط من أجل وظيفتهم، بل من أجل شكل المعادلات الساحر، والحقائق الشعرية البسيطة التي تحتوي عليها.
في حين أنّ بعض المعادلات المشهورة، مثل E = mc ^ 2 لأينشتاين، تحوز معظم المجد العام كأشهَرِ معادلةٍ في تاريخ العِلم، فإنّ العديد من الصيغ الأقلّ شهرةً لها أبطالها بين العلماء. سأل موقع لايف ساينس Livescience الفيزيائيين والفلكيين وعلماء الرياضيات عن معادلاتهم المفضلة. وهذا ما وجدناه:
1-إنه أينشتاين يا سادة!
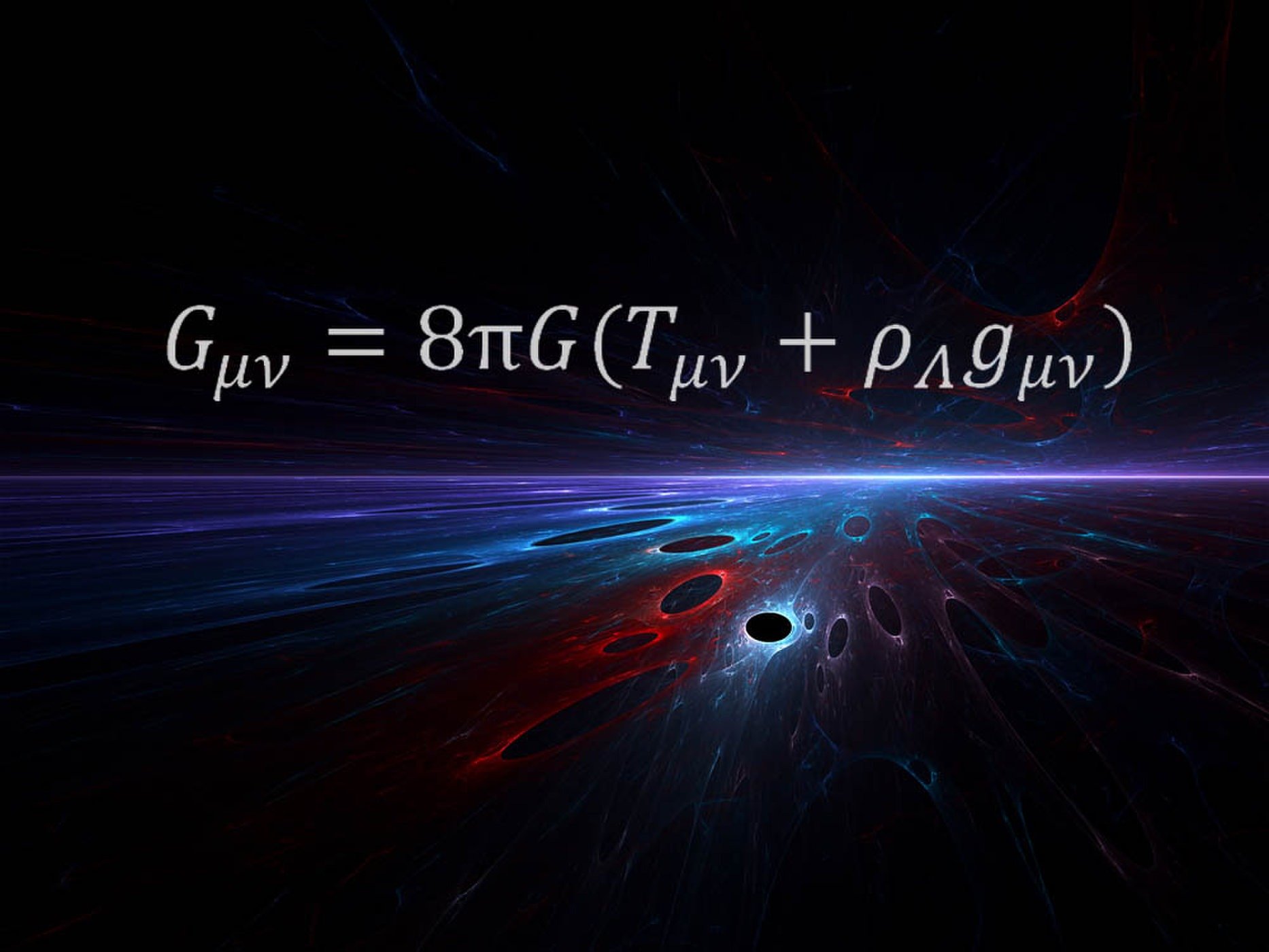
تمّت صياغة المعادلة أعلاه بواسطة آينشتاين كجزء من نظريته الرائدة، النسبية العامة، في عام 1915. أحدثت ثورة في كيفية فهم العلماء الجاذبية من خلال وصف القوة بأنها تشويه نسيج الزمكان (the fabric of space and time).
وقال ماريو ليفيو (Mario Livio) الفيزيائيّ الفلكي بمعهد علوم التلسكوب الفضائي الذي رشّح المعادلة على أنها المفضلة لديه: «ما زال من المدهش بالنسبة لي أنّ واحدة من المعادلات الرياضية يمكن أن تصف ما هو الفضاء.» وأضاف: «كلّ عبقرية آينشتاين الحقيقية تتجسد في هذه المعادلة».
يصف الجانب الأيمن من هذه المعادلة محتويات الطاقة لكوننا (بما في ذلك “الطاقة المظلمة” التي تدفع التسارع الكوني الحالي)، يوضّح ليفيو: «يصف الجانب الأيسر هندسة الزمكان. وتعكس المساواة حقيقة أنه في نظرية آينشتاين العامة، تُحدِّد الكتلة والطاقة هندسة الزمكان، وبالتوازي مع الانحناء، الذي هو مظهر لما نُسمّيه بالجاذبية».
إعلان
وقال كايل كرانمر (Kyle Cranmer)، الفيزيائي بجامعة نيويورك، «إنها معادلة أنيقة للغاية»، مضيفًا أنّ المعادلة تكشف العلاقة بين الزمكان والمادة والطاقة. «هذه المعادلة تُخبرك عن كيفية ارتباطها -كيف يُشوّه وجود الشمس الزمكان بحيث تدور الأرض حول الشمس، إلخ. كما تُخبرك كيف تطوّر الكون منذ الانفجار الكبير وتتنبأ المعادلة أن تكون هناك ثقوب سوداء».
2-النموذج القياسي في فيزياء الجسيمات

معادلة أخرى من نظريات الفيزياء السائدة، النموذج القياسي (standard model) والذي يصف مجموعة الجسيمات الأساسية التي يُعتقد أنها تشكّل عالمنا.
يُمكن تضمين هذه النظرية في معادلة رئيسة تُسمى النموذج القياسي لاغرانجان (the standard model Lagrangian)، (سُمّي على اسم عالم الرياضيات والفلكي الفرنسي من القرن الثامن عشر، جوزيف لويس لاغرانج)، والتي تمّ اختيارها من قِبَل الفيزيائي النظري لانس ديكسون (Lance Dixon) من مختبر سلاك الوطني في كاليفورنيا، باعتبارها الصيغة الرياضية المفضلة لديه.
وقال ديكسون: «لقد وصفتْ بنجاح جميع الجسيمات الأولية والقوى التي لاحظناها في المختبر حتى الآن -ما عدا الجاذبية، وهذا يشمل بالطبع بوزون هيغز المكتشف حديثًا (ويدلّ عليه الرمز فاي-phi في المعادلة). إنه متوافق تمامًا مع ميكانيك الكم والنسبية الخاصة».
ومع ذلك، لم تكن نظرية النموذج المعيارية مُوحّدة مع النسبية العامة، وهذا هو السبب في أنها لا تستطيع وصف الجاذبية.
3-حساب التفاضل والتكامل

في حين تصف المعادلتان السابقتان جوانب معيّنة من كوننا، يُمكن تطبيق معادلة رائعة أخرى على جميع أنواع المواقف. تُشكل النظرية الأساسية في حساب التفاضل والتكامل العمود الفقريّ للأسلوب الرياضيّ المعروف باسم حساب التفاضل والتكامل، وتربط بين فكرتيه الرئيسيتين، مفهوم التكامل ومفهوم المشتقّ.
وقالت ميلكانا براكالوفا تريفيثيك (Melkana Brakalova-Trevithick)، رئيسة قسم الرياضيات في جامعة فوردهام، والتي اختارت هذه المعادلة على أنها المعادلة المُفضّلة لها: «بكلمات بسيطة، تقول المعادلة أنّ التغيير الصافي لكمية بسيطة ومستمرة، مثل المسافة المقطوعة، خلال فترة زمنية معينة (أي الفرق في قيم الكمية في نقاط نهاية الفاصل الزمني) يساوي معدّل التغيّر في هذه الكمية ، أي تكامل السرعة». وأضافت: «تسمح لنا النظرية الأساسية في حساب التفاضل والتكامل (FTC) بتحديد صافي التغير خلال فترة زمنية استنادًا إلى معدل التغيير خلال الفترة الزمنية بأكملها».
ولكن- من وجهة نظري- لتدرك جمال حساب التفاضل والتكامل عليك بكتاب مخصّص للموضوع، وقلم رصاص، وحزمة ورق أبيض، وكوب شاي ثقيل، ولتعيش مع تدريبات على التفاضل والتكامل في عالم تجريديّ رائع.
بدأت بذور التفاضل والتكامل في العصور القديمة، ولكن تمّ وضع الكثير منها في القرن السابع عشر بواسطة إسحاق نيوتن، الذي استخدم حساب التفاضل والتكامل لوصف حركة الكواكب حول الشمس.
ونلتقي في الجزء التاني مع معادلات أجمل.
إعلان
