كيف بدأ التوبولوجي؟!
من اويلر الى نوبل

تظهر أعراض الـ overthinking على كثير من الناس بعد منتصف الليل، وتظهر معهم أسئلة تكون الإجابة عليها مستحيلة، ومن أشهر أسئلة الـ overthinking سؤال “كيف بدأ الخلق؟”. ولكن في المجتمع الرياضي تظهر أسئلة الـ overthinking بشكل مختلف متأثرين بطبيعة عملهم، فتصبح الأسئلة كـ “كيف بدأ التوبولوجي؟!”
والفرق بين السؤالين أنّ السؤال الأول يصعب الاتفاق على إجابة واحدة له، أما السؤال الثاني فيمكن الإجابة عليه، وهو ما سوف نتناوله في هذا المقال.
ماذا تعنى كلمة توبولوجي؟ ماهو التوبولوجي رياضيًا؟ كيف نشأ؟ ما أهميته؟ وما هي التطبيقات المستفادة منه؟ … الخ
كلّ هذه الأسئلة سوف تدور في ذهنك وأنت تقرأ الآن، في هذا المقال سنحاول الإجابة عن معظمها. وأول ما سوف نتعرف عليه هو تاريخ نشأه التوبولوجي، أو بمعنى أصحّ “كيف بدأ التوبولوجي؟”
وكعادة التاريخ، سوف يتمّ ذكر أفكار وأحداث تمّت في أزمنة مختلفة أدّت إلى ظهور مفهوم التوبولوجي.
إعلان
أولًا: أصل كلمة توبولوجي Topology
تنقسم كلمة التوبولوجي إلى مقطعين المقطع الأول (Topo) التي تعود إلى أصل يوناني إلى (Topos) والتي تعني “مكان”(Place)، والمقطع الثاني هو (logy) والتي تعود لأصل يوناني (Logos) وتعني “دراسة” (Study). إذًا فالتوبولوجي هو الهندسة الحديثة في دراسة جميع التراكيب والمكونات للفضاءات المختلفة أو بمعنى أبسط هو “علم دراسة المكان”.
- ولتوضيح مفهوم التوبولوجي فلنتخيّل أنّك تمتلكُ أشكالًا هندسية، مثل المربع والمثلث، وأردْتَ أن تعرف أوجه الاختلاف بينهما. طبقًا للهندسة التقليدية فكلّ شكل له خصائص معينة ومنها تستطيع أن تحصل على أوجه الاختلاف بين المربع والمثلث. ولكن طبقًا للـتوبولوجي فالمربع والمثلث لا يوجد بينهما اختلاف واحد، أي أنهما متكافئَين، في التوبولوجي تتمّ معاملة الأشكال التي تمتلك نفس عدد الفجوات (holes)، نفس المعاملة ولا يوجد بينها أيّ اختلاف لأنه يمكنك بكلّ بساطة الحصول على المثلث من المربع أو العكس عن طريق إعادة تشكيلة، وهذا هو الفارق الجوهري بين الهندسة التقليدية وهندسة التوبولوجي.
ويمكنك تخيّل عملية التحويل من خلال الضعط على الصورة

ثانيًا: فروع التوبولوجي؟
يتفرع التوبولوجي لفروع كثيره أهمها:
1) التوبولوجي النقطية (point-set Topology):
وهو الفرع الذي يهتمّ بالتوبولوجي العامة من ناحية خصائص الفضاء من ناحية التراكيب.
2) التوبولوجي الجبرية (Algebraic Topology):
وهو الفرع الذي يهتمّ بشكل عام في دراسة درجات الترابط من خلال التراكيب الجبرية، مثل دراسة علم الهمولوجي (Homology).
3) التوبولـوجي الهندسية (Geometric Topology):
وهو الفرع الذي يهتمّ في دراسة Manifolds (بنية رياضية كلّ نقطة فيها لها جوار يكون هميومورفيك إلى الفضاء الإقليدي) (ويهتمّ بالأبعاد حسب أبعاد الفضاء الإقليدي).
ثالثًا: كيف نشأ التوبولوجي؟
قبل أن نتعرف على تاريخ نشأة التـوبولوجي يجب أن تعرف أنّ الوصول لنظرية ما أو قانون ما في الرياضيات يحتاج الكثير من السنين للتأكد من صحّته، ويمكن أن يتعاقب شخصان أو أكثر على قانون ما للتأكد من صحته والاعتراف به، إذًا فالوصول لنوع جديد من الهندسة (كالتبولوجي) لم يتمّ في ليلة وضحاها بل بدأ بفكرة أو لغز، وتمّ تطويرها على مرّ العصور للوصول لشكل نهائي جديد ومن ثم يتمّ الاعتراف به، وهذا ما حصل فعلًا مع التوبولوجي، كما سنذكر تاليًا.
متى ظهرت كلمة التوبولوجي؟
أول من صاغ مصطلح التبولوجي هو الألماني (جوهان بندكت) عام 1847، أما التوبولوجي الحديث الذي يعتمد اعتمادًا كليًّا على مفهوم نظرية المجموعات التي أسسها كانتور فقد ظهر في أواخر القرن التاسع عشر، ومن بعدها بدأ تطورعلم التوبولوجي على هذا الأساس.
لغز أويلر!
تقع مدينة كونيغسبرغ الروسية (كالينينغراد-روسيا حاليًا) بين نهرين، وتتّصل بباقي المدن عن طريق سبعة جسور كما هو موضّح في صورة رقم 1. وكان سكّان المدينة يقومون بطرح ألغاز معتمدين فيها على هيئة الجسور التي تربطهم بالمدن الأخرى، وكان أشهر الألغاز وقتها كالآتي:
“هل يمكنك اجتياز الجسور السبعة دون عبور أيّ جسر مرتين؟”
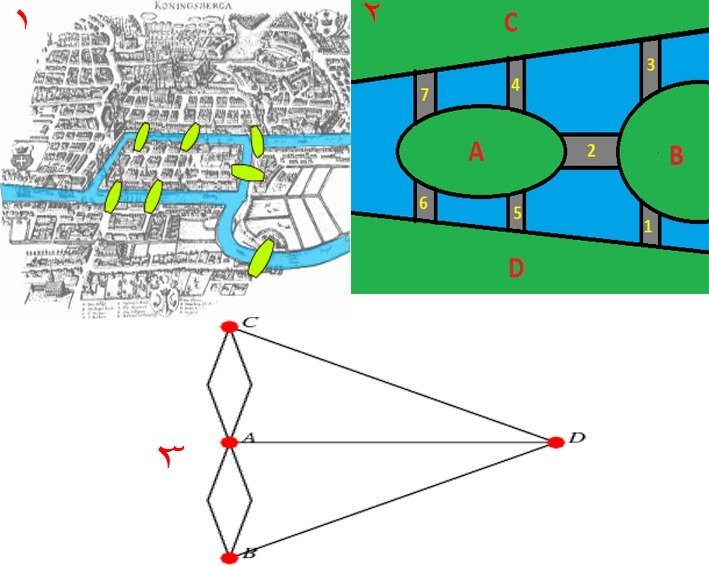
فشل كثير من الناس للوصول لحلّ، حتى وصل اللغز لعالِم الرياضيات الشهير (ليونهارت أويلر) عام 1736، ولكن أويلر لم يستطع الإجابة على اللغز لأنّ الإجابة لم تكن موجودة! بمعنى أنّه لا يمكنك اجتياز الجسور السبعة دون عبور أيّ جسر مرتين.
• ولكن كيف عرف أويلر أنّ الإجابة غير موجودة (مستحيلة)؟
قام أويلر باعتبار المدن نقاطًا والجسور أسهمًا، كما في الصورة رقم 3، ووضع قانونًا للمسار ينصّ على أنه يمكنك أن تمرّ على كلّ الخطوط إذا احتوت كلّ نقطة على عدد متساوٍ من الخطوط، أو بمعنى آخر إذا احتوت كلّ نقطة على عدد فرديّ من الخطوط فلن تستطيع أن تعبر كلّ الجسور، فإذا نظرت للصورة رقم 3 ستلاحظ أنّ النقط C وB وD تحتوي على 3 خطوط بينما النقطة A تحتوى على 5 خطوط وبالتالي لن تستطيع أن تجتاز كلّ الجسور دون عبور أيّ جسر مرتين.
• وهنا نأتي للسؤال المهمّ: كيف ساعد هذا الحلّ في ظهور التوبولوجي؟
الصورة رقم 3 تحتوي على ثلاثة خطوط طويلة وباقي الخطوط قصيرة إلى حدّ ما، فماذا لو قمنا بتغيير الأطول بحيث تصبح الخطوط الطويلةُ قصيرةً والقصيرةُ طويلةً … هل سوف يؤثر هذا على حلّ اللغز؟
بالطبع لا.. مهما تغيّرت الأطوال أو الأشكال التي يمكن صناعتها عن طريق الخطوط (الجسور) لن يتغير الناتج. وبالتالي فإنّ “جوهر الأجسام لا يتغير عندما تكبر أو تصغر”.
ولكن لو قمنا بإزالة خطّ أو إزالة نقطة (فجوة) فجوهر الشكل سيتغير بكل تأكيد، وهذه هي طريقة عمل التـوبولوجي؛ كما ذكرنا في مثال المربع والمثلث فكلاهما لا يحتوي على أيّ فجوات وبالتالي فهُما نفس الشيء بالنسبة للتوبولوجي. ولكن هل يمكن اعتبار الكوب والكرة نفس الشيء؟
الكرة لا تحتوي على أيّ ثقوب بينما الكوب يحتوي على ثقب واحد وبالتالي لا يمكن اعتبار الكوب كرة أو العكس، ولكن يمكن اعتبار الكوب كعكة دونت أو العكس.. لدرجة جعلت الناس يطلقون الدعابات على الشخص المتخصص في التوبولوجي كالآتي:
“A topologist is a person who cannot tell a coffee cup from a doughnut ”
” الشخص التوبولوجي لا يستطيع أن يفرق بين الكوب وكعكة الدونت”

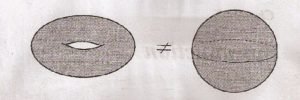
رابعًا: التطبيقات المستفادة من التوبولوجي؟
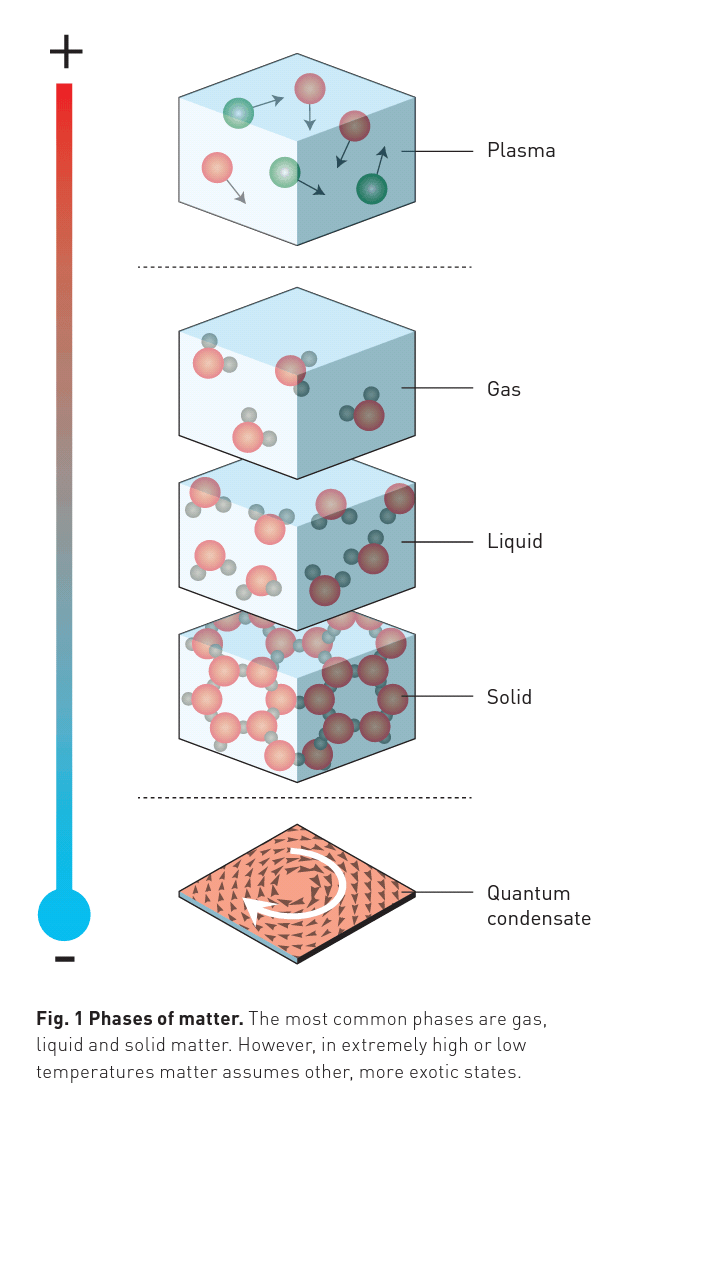
جائزة نوبل في الفيزياء 2016

حصل كل من (ديفيد ثوليس)الفيزيائي بجامعة واشنطن و(فريدرك دنكان هالدين) الفيزيائي بجامعة برينستون و(مايكل كوستيرليتز) الفيزيائي بجامعة براون بجائزة نوبل في الفيزياء 2016م؛ عن إنجازاتهم النظرية في فهم أغرب حالات المادة في درجات حرارة القريبة من الصفر المطلق
ولكن كيف ساعد التوبولوجي في هذا الاكتشاف؟
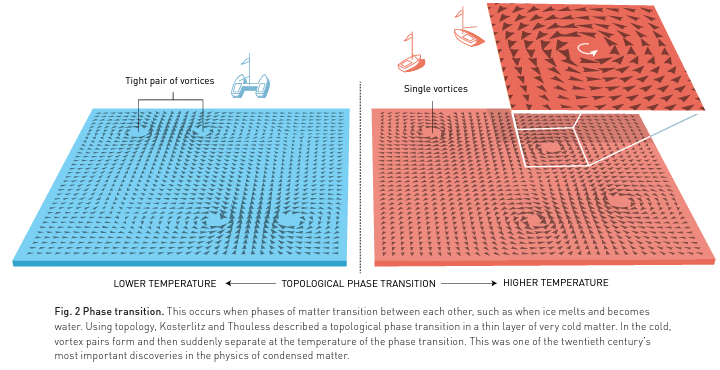
- بالرغم من صعوبة التوبولوجي إلا أنه يصبح مفيدًا وفعّالًا عند استخدامه في الفروع الأخرى كما حدث في الاكتشاف السابق، كما أنه يعتبر من الفروع الحديثة القابلة للتطور، وهذا يفتح المجال للعلماء والباحثين للاستفادة منه والعمل على تطويره لخدمة الفروع الأخرى.
• المصادر
إعلان