أجملُ معادلات العلمِ (الجزء الثاني)

استكمالًا لما بدأناه في الجزء الأول من سلسلة “أجمل معادلات العلم”…
4- نظرية فيثاغورس.

منذُ زمن بعيد، اكتشف عالم رياضيات يونانيّ اسمه: فيثاغورث خاصية مثيرة للاهتمام حول المثلثات الصحيحة. يُطلق على هذه الخاصية -التي لديها العديد من التطبيقات في مجالات العلوم والفنّ والهندسة والهندسة المعمارية- الآن نظرية فيثاغورس.
ويُطلق على نظرية فيثاغورث مَثَل: (oldie but goodie)، والذي يعني أنها نظرية قديمة ولكنها مازالت مُستخدمة، ويتعلمها كلّ طالب في المراحل الدراسية الأولى.
تصف هذه الصيغة كيف أنّ مربع طول الوتر، أي الجانب الأطول من المثلث بالنسبة لأي مثلث قائم الزاوية، يساوي مجموع مربعات أطوال الضلعين الآخرين.
إعلان
وقالت عالمةُ الرياضيات داينا تايمينا (Daina Taimina) من جامعة كورنيل: “الحقيقة الرياضية الأولى التي أدهشتني كانت نظرية فيثاغورس”.
وأضافت: “كنت طفلة آنذاك، وبدت لي مدهشة للغاية؛ لأنها تعمل في الهندسة وتعمل مع الأرقام!”
5- معادلة أويلر.
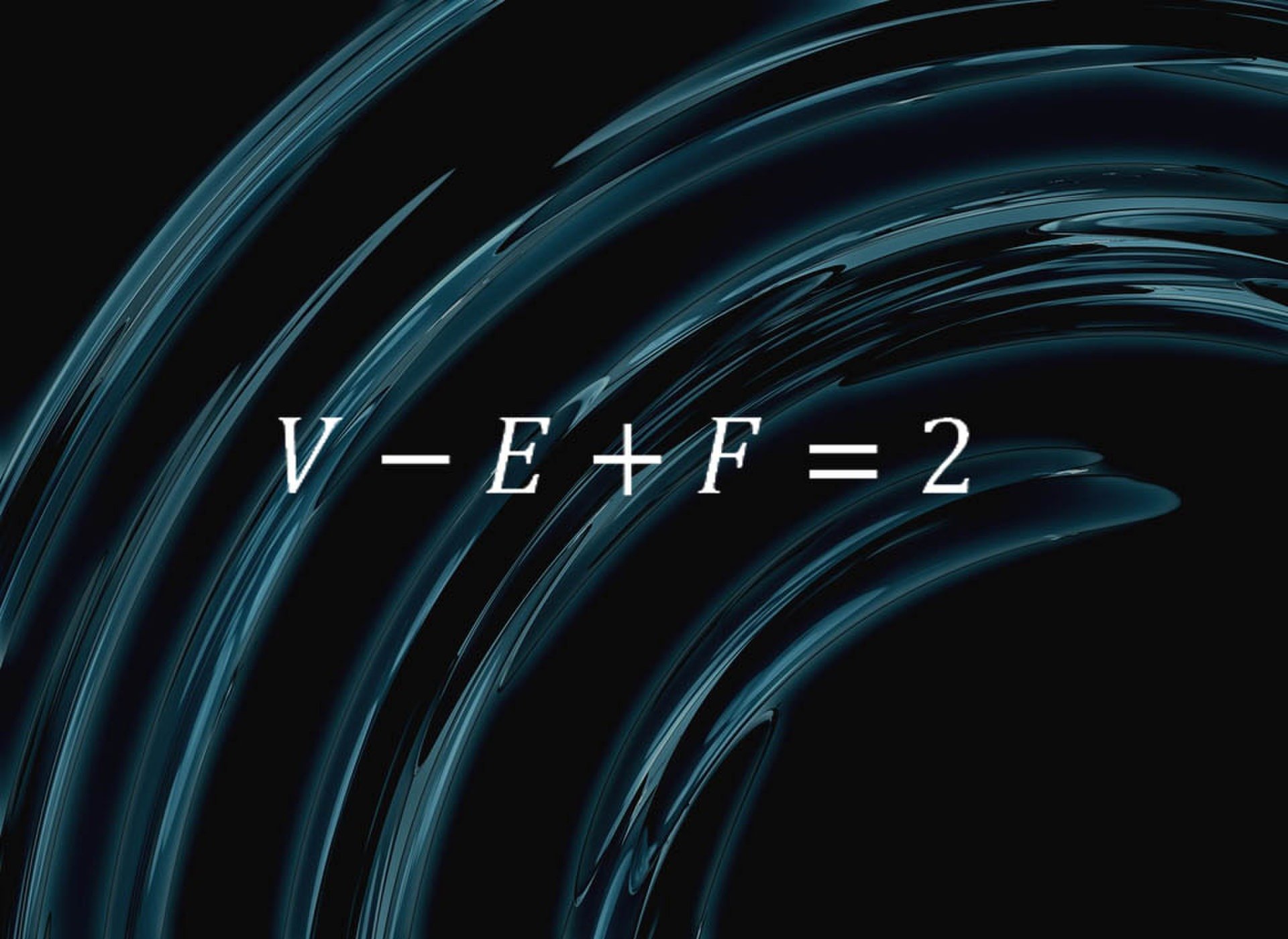
تحتوي هذه الصيغة البسيطة على شيء خالص حول طبيعة المجالات:
وقال كولن آدامز (Colin Adams) عالم رياضيات في كلية ويليامز في ماساتشوستس: “تقول المعادلة أنه إذا قمت بتقطيع سطح الكرة إلى الوجوه والحوافّ والرؤوس، ودع F يكون عدد الوجوه، E عدد الحواف وV عدد القمم؛ ستحصل دائمًا على V – E + F=2”.
وأضاف: “هكذا على سبيل المثال عند أخْذ شكل رباعيّ الأسطح والذي يتألف من أربعة مثلثات، وستةِ حواف، وأربعة رؤوس”.
وأوضح آدامز: ومن هذا المنطلق، يمكن قطع الكرة إلى أربعة أوجه وستة حوافٍ وأربعة رؤوس.
ونرى أنّ لـ V – E + F = 2 نفس التأثير لهرم مع خمسة وجوه، أربعة على شكل المثلث وواحد على شكل المربع، ثمانية حواف وخمسة رؤوس، وأي مجموعة أخرى من الوجوه والحواف والرؤوس.
وقال آدامز: حقيقة رائعة للغاية! إنّ توافقية القمم والحواف والوجوه شيء أساسي للغاية حول شكل الكرة.
6- النسبية الخاصة.
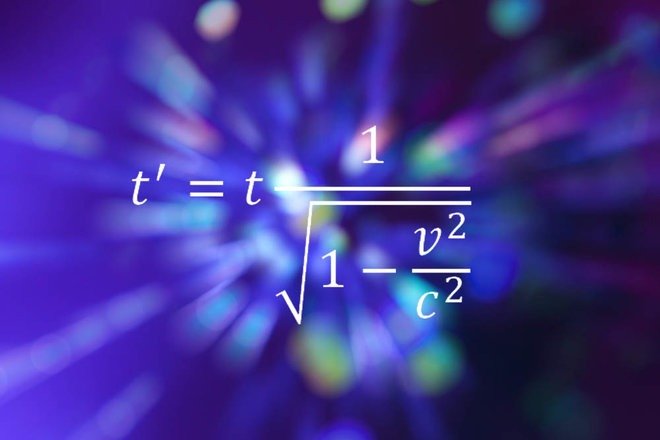
يعود آينشتاين مرة أخرى إلى القائمة بصيغته للنسبية الخاصة، والتي تصف كيف أنّ الزمان والمكان ليسا مفهومان مطلقان؛ بل نسبيان، ويعتمدان على سرعة المراقب.
تُظهر المعادلة أعلاه كيفية تمدّد الوقت أو تباطؤه كلّما كان الشخص أسرع في أي اتجاه.
وقال بيل موراي (Bill Murray) وهو عالم فيزياء الجسيمات في مختبر سيرن في جنيف: النقطة هي في الحقيقة بسيطة جدًا، ولا يوجد شيء في المعادلة لا يمكن لطالب مستوى A القيام به، لا مشتقّات معقدة أو استخدام للجبر لكن ما تجسّده المعادلة هي طريقة جديدة تمامًا للنظر إلى العالم، وموقف كامل من الواقع وعلاقتنا به.
فجأةً اجتيح الكون الثابت غير المتغير واستُبدِل بعالَم شخصي مرتبط بما تلاحظه أنت، تنتقل من كونك خارج الكون، تنظر إلى الأسفل، إلى أحد المكونات داخله، لكنّ المفاهيم والرياضيات يمكن فهمها من قبل أي شخص يريد ذلك.
قال موراي أنه يفضل معادلات النسبية الخاصة على الصيغ الأكثر تعقيدًا في نظرية آينشتاين اللاحقة.
وقال: لايُمكنني أبدًا أن أتبع الرياضيات المُستخدمة في النسبية العامة.
7- …9 1.99999999

هذه المعادلة البسيطة والتي تنصّ على أنّ: الكمية 0.999 متبوعة بسلسلة لا نهائية من الرقم 9 تعادل واحد، هي المُفضلة لدى الرياضي ستيفن ستراغاتز Steven Strogatz من جامعة كورنيل.
وقال ستراغاتز: أحببت بساطتها، كم هي بسيطة!
قد يبدو كلامه مستفزًا بالنسبة لك ولكن هكذا الأرقام؛ تخطف قلب من تريده.
وأضاف: يعتقد كثيرٌ من الناس أنه لا يمكن أن يكون الرقم صحيحًا، المعادلة أيضًا متوازنة بشكل جميل؛ حيث يمثل الجانب الأيسر بداية الرياضيات، ويمثل الجانب الأيمن أسرار اللانهاية.
إعلان
