لماذا خلق الله العالَم في ستة أيام؟ الرياضيات تجيب!
نظرة تاريخية إلى الأعداد المثالية وأعداد ميرسين الأولية

ما هو العدد المثالي ؟
العدد المثالي هو العدد الصحيح الموجب الذي يساوي مجموع قواسمه عدا نفسه. وأصغر عدد مثالي معروف هو العدد 6 وقواسمه هي (1،2،3،6) إذا جمعنا القواسم عدا (6) سينتج 1+2+3=6
الأعداد المثالية قليلة ومتباعدة جدًّا، مثلًا الأعداد المثالية التالية هي 28، ثم 496، ثمّ 8128، ثمّ 33550336، والعدد التالي مؤلّف من تسعة منازل!

قصّة الأعداد المثالية
عرِف اليونانيون القدماء أمثال فيثاغورس وإقليدس الأعداد المثاليّة لكنهم لم يكتشفوا سوى أوّل أربعةٍ منها، كما أوجد إقليدس صيغةً عامّة تربط بين الأعداد المثاليّة والأعداد الأوليّة (ليس أيّ عددٍ أوّلي، بل أعداد ميرسين كما ستُعرَف لاحقًا)، الصيغة هي:
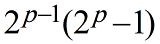
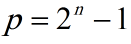
درَس فيثاغورس وتلاميذه الأعداد المثاليّة لإيمانهم بأنّها تشمل على خصائص روحيّة فريدة، حيث اعتبر بعضهم أنّ الأعداد التي تزيد عن مجموع قواسمها أعداد شرِهة وتشبه مخلوقاتٍ لديها عدّة أفواه، أمّا الأعداد التي تنقص عن مجموع قواسمها فهي أعداد ناقصة ومشوّهة، وبالتالي فالأعداد التي تساوي مجموع قواسمها هي الأعداد المثاليّة، وارتبط العدد 28 (العدد المثاليّ الثاني) بدورة القمر والشهر القمريّ من وجهة نظرهم.
فيما بعد ازداد تقدير هذه الأعداد لدرجة أنّ القدّيس أوغوستين قال
إعلان
إنّ الله خلق الكون في ستّة أيّام لأنّ العدد ستة عدد مثالي، وليس العكس أي لم يصبح العدد ستّة مثالي لأنّ الله خلق الكون في ستّة أيّام!
برهن أويلر العلاقة التي وضعها إقليدس بعد ألفي عام من وفاته، وهذا يدلّ على صعوبة العمل على هذه المجموعة الفريدة، لكن هذا لم يمنع العلماء من اكتشاف صيغ أخرى للأعداد المثاليّة، فقد توصّلوا لصيغة جميلة تعتمد على العدد المثلّثي وهي:
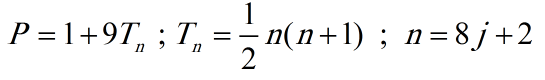
حيث P هو العدد المثالي، وT هو العدد المثلثي، والأعداد n,j أعداد صحيحة موجبة.
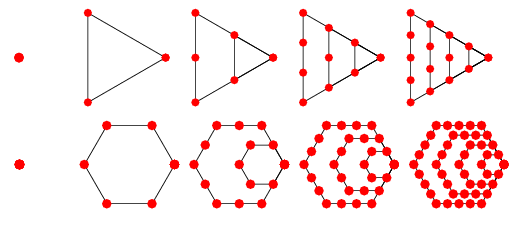
كما بُرهِن أيضًا على أنّ جميع الأعداد المثاليّة هي أعداد مسدّسة، مع الانتباه إلى أنّه ليس كلّ عدد مثلّثي أو عدد مسدّسي هو عدد مثالي بالضرورة.
أعداد ميرسين الأوليّة
من الطريف أنّ الأعداد المثاليّة التي يعتمد تعريفها على قواسمها ترتبط ارتباطًا وثيقًا بمجموعة من الأعداد الأوّليّة تُدعى أعداد ميرسين وهي أعدادٌ قليلة أيضًا ويبلغ عددها 51 عددًا، وهي الأعداد التي تُكتب بالصيغة التالية:
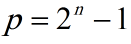
وعلى العموم كلّما اكتُشِف عدد أوّلي من أعداد ميرسين سيرافقه اكتشاف عدد مثالي جديد، لذلك فإنّ العمل على أعداد ميرسين أكثر جاذبيّة للباحثين، وهذا ما تفعله مجموعة GIMPS المختصّة بالبحث عن أعداد ميرسين الأولية الضخمة عبر تسخير جهود الباحثين الهواة وقدرات حواسيبهم عبر الإنترنت.
لماذا أعداد ميرسين؟
قد يتساءل البعض لماذا تعمل مجموعة كبيرة من الباحثين عبر الإنترنت على أعداد ميرسين بالذات؟
توجد عدّة أسباب، أوّلاً كما لاحظنا فإنّ أعداد ميرسين ستقودنا للأعداد المثاليّة، كما أنها أعداد أوّليّة بكلّ الأحوال، لذا فإنّ من يكتشف عددًا جديدًا سيُسجّل اسمه في قائمتين لا تحويان عددًا كبيرًا من الأسماء (أقلّ من 50 اسمًا حتى تاريخ كتابة هذا المقال) كما أنّ الطريق الأسرع للوصول للأعداد المثالية هو عن طريق أعداد ميرسين، لأنّ الميّزات الأخرى للأعداد المثاليّة لا تشكّل علامة فارقة كما تفعل أعداد ميرسين، فحيث إنّ كلّ عدد ميرسين جديد سيؤدّي حتمًا لعدد مثالي فإنّ الأعداد المثلثيّة أو الأعداد المسدّسة لن تفعل ذلك، أمّا طريقة جمع القواسم فهي تكاد تكون مستحيلة بعد الوصول لأكثر من 49 مليون خانة، وهي طريقة جيّدة لاختبار قدرات الحواسيب الجديدة!
ما هي الفائدة العمليّة من الأعداد المثاليّة؟
في الحقيقة لا توجد فائدة مباشرة منها، والرياضيّات عمومًا لا تعمل بهذه الطريقة، أي إنّ العلماء لا يبدأون العمل على المسائل من أجل فائدتها، بل من أجل المتعة، ثمّ يجدون لها تطبيقات فيما بعد، وبالنسبة للأعداد المثاليّة فهي أعداد جميلة وتتمتّع بخواصّ مغرية للعمل عليها كما أنّها تُعدّ صالحة حتّى الآن للبحث في مسائل غير محلولة، مثل البرهان على أنّ الأعداد المثاليّة منتهية أو غير منتهية، وكذلك هل الأعداد المثاليّة زوجيّة دومًا؟
رغم أنّ جميع الأعداد المثاليّة المكتشفة حتى الآن والبالغ عددها 51 عددًا، جميعها زوجيّة بل إنّها جميعًا تنتهي بالرقم (6) أو الرقم (8) وهذا يقابل في نظام العدّ الثنائي إمّا (0) أو (00)، رغم ذلك إلا أنّ الرياضيّين يفضّلون البراهين النظريّة الأكثر موثوقيّة حتى لو كانت أصعب، وحتّى ذاك الحين ستُدعى هذه الخواصّ في أفضل الأحوال “حدسيّات”.
قد يعجبك أيضًا: عدد أولي يتمتع بمزايا نادرة
إعلان
